Реферат: Моделирование линейных непрерывных систем в среде LabVIEW

Видим, что одно и то же аналоговое устройство может описываться отличающимися дискретными передаточными функциями.

В таблице 1 была приведена дискретная передаточная функция интегрирующей цепи (для которой К (р) = 1/ (1 + рТ)), полученной применением Z-преобразования. Найдем другие варианты дискретной передаточной функции интегрирующей цепи, отличающиеся методами численного интегрирования.

При использовании метода прямоугольников (1) в передаточную функцию K (p) = 1/ (1 + pT) вместо р нужно подставить (z - 1) /Δt. Тогда получим

	Δt/T z – (1 – Δt/T)

 

K (z) = 1/ (1 + (z - 1) T/Δt)      =.

Аналогично можно получить дискретные передаточные функции и для других методов численного интегрирования. Они представлены в таблице 3 Принято обозначение Δt/T = α

Таблица 3

Метод	K (z)
Z-преобразование	α z z - e-α
Метод прямоугольников (1)	α z - (1 - α)
Метод прямоугольников (2)	(α/ (1 + α)) z z - 1/ (1 + α)
Метод трапеций	(α / (2 + α)) (z + 1) z - (2 - α) / (2 + α)

Этим передаточным функциям соответствуют следующие рекуррентные формулы.

Для Z-преобразования

yk = e-αyk - 1 + αxk. (7)

Для численного интегрирования по методу прямоугольников (1)

yk = (1 - α) yk - 1 + αxk - 1.

Полученная формула совпадает с формулой для прямого метода Эйлера

Для численного интегрирования по методу прямоугольников (2)

yk = (1/ (1 + α)) yk - 1 + (α/ (1 + α)) xk. (8)

и по методу трапеций

yk = ( (2 - α) / (2 + α)) yk - 1 + (α/ (2 + α)) (xk + xk - 1). (9)

В лабораторной работе производится оценка ошибок цифрового моделирования для каждого из этих методов.

Моделирование линейных замкнутых систем

Нужно быть очень внимательным при выборе интервала дискретизации, когда моделируются замкнутые системы. В этих системах текущее значение входного процесса сравнивается со значением выходного процесса, рассчитанного по предыдущим значениям входного процесса. Это экстраполированное значение не должно значительно отличаться от входного процесса.

В противном случае возникают большие ошибки моделирования, а при большом интервале дискретизации процесс может стать неустойчивым. Выбор интервала дискретизации нужно связывать с полосой пропускания замкнутой системы.

Проводя аналогию с теоремой Котельникова, можно потребовать, чтобы Δf0,1Δt = 5 - 10, где Δf0,1 - полоса пропускания замкнутой системы по уровню 0,1.

Рассмотрим моделирование непрерывной замкнутой системы на конкретном примере, когда передаточная функция разомкнутой системы

К р(1 + рТ)

Кр (р) =.                                                              (10)

Такая модель часто используется при анализе ошибок в следящей системе.

Запишем дискретную передаточную функцию разомкнутой системы, заменяя интеграторы по методу прямоугольников (2). Для этого преобразуем передаточную функцию разомкнутой системы (5.10), поделив числитель и знаменатель на р2:

	К/р2 Т + 1/р

Кр (р) =.

Используя соотношения, приведенные в таблице (5.2), получим:

	К(Δt)2z/(z – 1)2 Т + Δt z/(z – 1)		b1z z2 + a1z + a2

Кр (z) =                                                =,                               (11)

где b1 = K (Δt) 2/ (T + Δt), a1 = - (2T + Δt) / (T + Δt), a2 = T/ (T + Δt).

Для моделирования устройства с передаточной функцией (11) используется БИХ-фильтр, коэффициенты числителя которого (Forward Coefficients) представляются массивом из двух элементов (0,b1), а коэффициенты знаменателя - массивом из трех элементов (1, a1,a2).

Специфика использования БИХ-фильтра заключается в том, что неизвестен целиком входной массив Х, а известен только текущий элемент, а следующий элемент рассчитывается с учетом значения текущего элемента выходного массива фильтра. В LabVIEW существует такой фильтр - IIR Filter PtByPt (IIR Filter Point By Point - БИХ-фильтр точка за точкой).

Рис.6

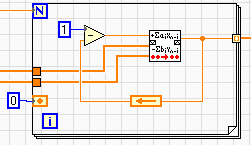
Вычисления БИХ-фильтром IIR Filter PtByPt производятся в цикле For

Loop (рис.5.6). В этом же цикле генерируется единичное входное воздействие. Автоматическое появление в цепи обратной связи регистра сдвига обусловлено тем, что рассчитанное значение выходного процесса используется для сравнения с входным только в следующем интервале дискретизации, то есть с запаздыванием на интервал дискретизации. В результате вычислений формируется массив переходной характеристики.

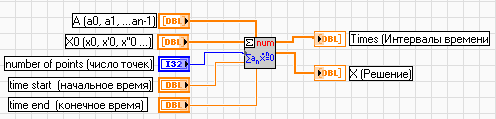
Для точного расчета переходной характеристики воспользуемся ВП ODE Linear nth Order Numeric - “Решение линейного обыкновенного дифференциального уравнения n-го порядка в численном виде” (рис.7).

Рис.7

ВП находит решение в виде суммы экспонент и вычисляет его для заданных точек. Поэтому решение точное.

Вход А представляет собой массив коэффициентов дифференциального уравнения в порядке увеличения степени производной. Коэффициент при производной самой высокой степени считается равным 1 и не требует ввода.

На вход Х0 подается массив начальных условий - начальные значения решения и его n - 1 - й производных.

Вход “число точек" задает число равноудаленных по времени точек между начальным и конечным временем

Выход Х содержит массив значений решения в равномерно расположенных по оси времени точках. Значение времени в этих точках выводится в массиве Times.

Дифференциальное уравнение замкнутой системы запишем по передаточной функции замкнутой системы:

	Кр(р) 1 + Кр(р)		К Тр2 + р + К

Кз (р) =                                            =                          (12)

Дифференциальное уравнение замкнутой системы

Td2y/dt2 + dy/dt + Ky = Kx

Запишем однородное дифференциальное уравнение, учитывая, что коэффициент при высшей производной должен быть равен 1

d2y/dt2 + (1/Т) dy/dt + (K/Т) y = 0

Для компьютерного решения этого уравнения нужно задать массив А = (К/Т, 1/Т). Чтобы получить переходную характеристику, нужно задать массив Х = ( - 1, 0) и к решению прибавить 1.

Полностью блок-схема программы моделирования замкнутой системы приведена на рис.8.

k

K

T

k

dt

Рис.8

Заключение

В основе технологии использования LabVIEW лежит комбинированное моделирование систем на ЭВМ, включающее аналитическое, имитационное и натурное.

Для аналитического моделирования характерно то, что алгоритм функционирования системы записывается в виде некоторых аналитических соотношений (алгебраических, интегро-дифференциальных, конечно - разностных и т.п.) или логических условий. При имитационном моделировании алгоритм функционирования системы воспроизводится во времени с сохранением логической структуры и последовательности протекания элементарных явлений, составляющих процесс. В настоящее время имитационное моделирование - наиболее эффективный метод исследования систем, а часто и единственный практически доступный метод получения информации о поведении системы, особенно на этапе ее проектирования.

Натурным моделированием называют проведение исследования на реальном объекте с возможностью вмешательства человека в процесс проведения эксперимента и последующей обработки результатов эксперимента на вычислительной технике.

Отличие модельного эксперимента от реального заключается в том, что в модельном эксперименте могут быть реализованы любые ситуации, в том числе "невозможные" и аварийные, что в силу разных причин бывает недопустимо при работе с реальными объектами. Все представленные виды моделирования могут быть реализованы с использованием системы программирования LabVIEW.

Список литературы

1.  Н.А. Виноградова, Я.И. Листратов, Е.В. Свиридов. "Разработка прикладного программного обеспечения в среде LabVIEW". Учебное пособие - М.: Издательство МЭИ, 2005.

2.  http://www.automationlabs.ru/

3.  http://digital. ni.com/

4.  http://www.labview.ru/

5.  http://ru. wikipedia.org/