 Реферат: Математическое моделирование как философская проблема
Реферат: Математическое моделирование как философская проблема
Если результаты моделирования подтверждаются и могут служить основой для прогнозирования процессов, протекающих в исследуемых объектах, то говорят, что модель адекватна объекту. При этом адекватность модели зависит от цели моделирования и принятых критериев.
Обобщенно моделирование можно определить как метод опосредованного познания, при котором изучаемый объект-оригинал находится в неком соответствии с другим объектом-моделью, причем модель способна в том или ином отношении замещать оригинал на некоторых стадиях познавательного процесса. Стадии познания, на которых происходит такая замена, а также формы соответствия модели и оригинала могут быть различными:
Моделирование как познавательный процесс, содержащий переработку информации, поступающей из внешней среды, о происходящих в ней явлениях, в результате чего в сознании появляются образы, соответствующие объектам.
Моделирование, заключающееся в построении некоторой системы-модели (второй системы), связанной определенными отношениями подобия с системой-оригиналом (первой системой), причем в этом случае отображение одной системы в другую является средством выявления зависимостей между двумя системами, отраженными в соотношениях подобия, а не результатом непосредственного изучения поступающей информации.
Следует отметить, что с точки зрения философии моделирование – эффективное средство познания природы. Процесс моделирования предполагает наличие:
объекта исследования;
исследователя, перед которым поставлена конкретная задача;
модели, создаваемой для получения информации об объекте и необходимой для решения поставленной задачи.
По отношению модели исследователь является, по сути дела, экспериментатором, только в данном случае эксперимент проводится не с реальным объектом, а с его моделью. Надо иметь в виду, что любой эксперимент может иметь существенное значение в конкретной области науки только при специальной его обработке и обобщении. Единичный эксперимент никогда не может быть решающим для подтверждения гипотезы, проверки теории. Следует помнить о том, что критерием истины являются опыт, практика, экспериментальное исследование.
Вычислительный эксперимент, его определение и основные этапы.
Академик А. А. Самарский, один из основоположников вычислительной математики и математического моделирования в нашей стране, создатель ведущей школы в области математического моделирования, понимал под вычислительным экспериментом такую организацию исследований, при которой на основе математических моделей изучаются свойства объектов и явлений, проигрывается их поведение в различных условиях и на основе этого выбирается оптимальный режим[5]. Другими словами, вычислительный эксперимент предполагает переход от изучения реального объекта к изучению его математической модели. Такой моделью, как правило, является одно или несколько уравнений. Более строго математические модели будут определены ниже.
Впервые вычислительный эксперимент начал использоваться для изучения таких процессов, экспериментальное исследование которых невозможно или затруднено. Например, в 40-50 годы XX столетия академик М.В. Келдыш разрабатывает математическое описание космических полетов.
К основным преимуществам вычислительного эксперимента можно отнести следующие:
Возможность исследования объекта без модификации установки или аппарата.
Возможность исследования каждого фактора в отдельности, в то время как в реальности они действуют одновременно.
Возможность исследования нереализуемых на практике процессов.
Вычислительный эксперимент включает в себя следующие этапы (см. рисунок 1):
Физическое описание процесса, то есть уяснение закономерности протекаемых явлений.
Разработка математической модели.
Алгоритм или метод решения уравнений.
Разработка программ.
Проведение расчетов, анализ результатов и оптимизация.
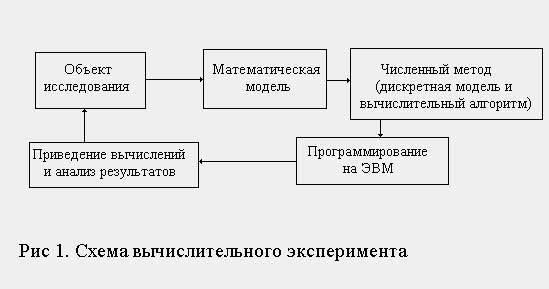
Тем самым основу вычислительного эксперимента составляет триада: модель – алгоритм - программа. Опыт решения крупных задач показывает, что метод математического моделирования и вычислительный эксперимент соединяют в себе преимущества традиционных теоретических и экспериментальных методов исследования.
Стоит заметить, что на практике результаты первых расчетов, как правило, весьма далеки от реальных. Поэтому происходит постоянное усовершенствование алгоритма, уточнение математической модели до совпадения с какими-то тестовыми или контрольными данными. Этот этап, называемый идентификацией математической модели, всегда присутствует в вычислительном эксперименте. Поэтому нельзя говорить об одной модели любого явления. Всегда существует иерархия математических моделей, начиная от простых и кончая более сложными. Следует выбирать некоторый уровень сложности модели, соответствующей данной конкретной задаче.
Понятие математического моделирования как методологии научных исследований
Под математическим моделированием, в узком смысле слова, понимают описание в виде уравнений и неравенств реальных физических, химических, технологических, биологических, экономических и других процессов. Для того чтобы использовать математические методы для анализа и синтеза различных процессов, необходимо уметь описать эти процессы на языке математики, то есть описать в виде системы уравнений и неравенств.
Как методология научных исследований математическое моделирование сочетает в себе опыт различных отраслей науки о природе и обществе, прикладной математики, информатики и системного программирования для решения фундаментальных проблем. Математическое моделирование объектов сложной природы – единый сквозной цикл разработок от фундаментального исследования проблемы до конкретных численных расчетов показателей эффективности объекта. Результатом разработок бывает система математических моделей, которые описывают качественно разнородные закономерности функционирования объекта и его эволюцию в целом как сложной системы в различных условиях. Вычислительные эксперименты с математическими моделями дают исходные данные для оценки показателей эффективности объекта. Поэтому математическое моделирование как методология организации научной экспертизы крупных проблем незаменимо при проработке народнохозяйственных решений. (В первую очередь это относится к моделированию экономических систем[6]).
По своей сути математическое моделирование есть метод решения новых сложных проблем, поэтому исследования по математическому моделированию должны быть опережающими. Следует заранее разрабатывать новые методы, готовить кадры, умеющие со знанием дела применять эти методы для решения новых практических задач.
Математическая модель может возникнуть тремя путями:
В результате прямого изучения реального процесса. Такие модели называются феноменологическими.
В результате процесса дедукции. Новая модель является частным случаем некоторой общей модели. Такие модели называются асимптотическими.
В результате процесса индукции. Новая модель является обобщением элементарных моделей. Такие модели называют моделями ансамблей.
Процесс моделирования начинается с моделирования упрощенного процесса, который с одной стороны отражает основные качественные явления, с другой стороны допускает достаточно простое математическое описание. По мере углубления исследования строятся новые модели, более детально описывающие явление. Факторы, которые считаются второстепенными на данном этапе, отбрасываются. Однако, на следующих этапах исследования, по мере усложнения модели, они могут быть включены в рассмотрение. В зависимости от цели исследования один и тот же фактор может считаться основным или второстепенным.
Математическая модель и реальный процесс не тождественны между собой. Как правило, математическая модель строится с некоторым упрощением и при некоторой идеализации. Она лишь приближенно отражает реальный объект исследования, и результаты исследования реального объекта математическими методами носят приближенный характер. Точность исследования зависит от степени адекватности модели и объекта и от точности применяемых методов вычислительной математики.
Схема построения математических моделей следующая:
Выделение параметра или функции, подлежащей исследованию.
Выбор закона, которому подчиняется эта величина.
Выбор области, в которой требуется изучить данное явление.
Классификация математических моделей
Существуют всевозможные классификации математических моделей. Выделяют линейные и нелинейные модели, стационарные и динамические, модели, описываемые алгебраическими, интегральными и дифференциальными уравнениями, уравнениями в частных производных. Можно выделять классы детерминируемых моделей, вся информация в которых является полностью определяемой, и стохастических моделей, то есть зависящих от случайных величин и функций. Так же математические модели различают по применению к различным отраслям науки.
Рассмотрим следующую классификацию математических моделей[7]. Все математические модели разобьем условно на четыре группы.
I. Модели прогноза или расчетные модели без управления. Их можно разделить на стационарные и динамические.
Основное назначение этих моделей: зная начальное состояние и информацию о поведение на границе, дать прогноз о поведении системы во времени и в пространстве. Такие модели могут быть и стохастическими.
Как правило, модели прогнозирования описываются алгебраическими, трансцендентными, дифференциальными, интегральными, интегро-дифференциальными уравнениями и неравенствами. Примерами могут служить модели распределения тепла, электрического поля, химической кинетики, гидродинамики.


