 Реферат: Генетический алгоритм глобальной трассировки
Реферат: Генетический алгоритм глобальной трассировки
ПТ=ПИ+ПК.
Далее ко всем индивидуальнастям ПТ применяется оператор мутации. Для всех индивидуальностей популяции ПМ , образовавшихся в результате мутации расчитывается фитнесс. Заключительным этапом в пределах одного поколения является процесс редукции популяции ПТ=ПИ+ПК+ПМ до размеров ПИ на основе селективного отбора. Селекция осуществляется на основе “принципа рулетки”.
Вероятность выбора индивидуальности определяется как:
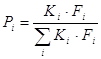
С помощью коэффициентов Кi, которые для «лучших» индивидуальностей имеют большие значения, чем у «худших», достигаются увеличение вероятности выбора «лучших» индивидуальностей.
Временная сложность алгоритма определяется общими (подготовительными) затратами to и затратами в пределах каждого поколения td . Общие затраты складываются из затрат на построении минимальных связывающих деревьев td ,формирование вариантов реализации ребер tb ,и формирования исходной популяции tи: to=td+tb+tи.
Затраты на построение МСД находятся в зависимости от числа МСД. С другой стороны при построении конкретного МСД затраты пропорциональны квадрату числа связываемых вершин . Учитывая , что число ребер n всех МСД пропорционально числу МСД , можно считать, что оценка ВСА tо лежит в пределах О(n)-O(n2), причем чем больше n тем ближе к О(n).
Затраты в пределах поколения tn складываются из затрат на операторы кроссинговера tк , мутации tm ,расчета фитнесса tф и селекции tс .
Как уже указывалось выше затраты tк ,tм и tф при обработке одной хромосомы имеют линейную зависимость от n . tс имеет линейную зависимость от объема популяции М . Тогда временные затраты в пределах поколения имеют оценку О(n×M). Для Т генераций временная сложность алгоритма имеет оценку О(n×M×T) . Учитывая что параметры М и Т сравнимы или значительно меньше n, можно считать , что оценка временной сложности всего алгоритма в целом лежит в пределах О(n2)-O(n3).
4. Экспериментальные исследования генетического алгоритма глобальной трассировки
Алгоритм глобальной трассировки был реализован на языке С++, экспериментальные исследования проводились на ЭВМ типа IBM PC/AT Pentium 133.
При проведении экспериментальных исследований преследовались две цели:
Первой целью являлось исследование механизмов генетического поиска для задачи глобальной трассировки. Для достижения этой цели исследовалось влияние управляющих операторов, таких как: размер популяции М, число поколений Т, вероятность мутации РМ, вероятность кроссинговера РК. В результате этих исследований определялось такое сочетание значений этих параметров, которое обеспечивает наивысшую эффективность генетических процедур для задачи глобальной трассировки.
Второй целью являлось исследование собственно, эффективности разработанного генетического алгоритма. Исследовались влияния таких параметров, как число вариантов маршрутов для каждого ребра.
Для проведения исследований были синтезированы 5 тестовых примеров.
Основные характеристики примеров.
Использовалось КП с размерами 10*10 (10 дискретов по горизонтали и 10 дискретов по вертикали). Выводы, связываемые цепями, размещались внутри дискретов. В каждом дискрете только один вывод одной цепи. Число выводов, связываемых одной цепью - от 2 до 5. В один дискрет назначалось до 10 выводов. Среднее число цепей - 200 -250. Назначение выводов в дискреты осуществлялось случайным образом.
Оптимизация проводилась по критерию:
F1=![]() ("i)[Cmin£Ci=ai-bi]
("i)[Cmin£Ci=ai-bi]
Если оказывалось, что Сmin<0, то оптимизация автоматически переключалась на критерий F2 = m - g, где g- число ребер, проходящих через грани с отрицательным значением Сmin.
Для нахождения наилучшего сочетания таких параметров, как Рм, Рк, М и Т, а также для выбора последовательности и типа генетических операторов экспериментальные исследования проводились следующим образом:
Для каждого примера сначала фиксировался параметр Рм и изменялись параметры Рк и М. Проводилась серия из десяти экспериментов для каждого фиксированного набора параметров. Затем фиксировался параметр Рк. Формирование исходной популяции осуществлялось следующим образом. Для каждой цепи строилось МСД. Если в процессе его построения возможно несколько альтернатив, то выбиралась первая. Для каждого ребра каждого дерева формировался набор вариантов маршрутов. Для каждой хромосомы исходной популяции выбор вариантов осуществлялся случайным образом.
При проведении испытаний для каждого эксперимента фиксировался номер генерации, после которой не наблюдалось улучшения оценки. В каждой серии из десяти испытаний фиксировались минимальные, максимальные и средние числа генераций.
Для каждой серии испытаний определялось лучшее решение, которое фактически являлось оптимальным. Затем фиксировалось число испытаний, при которых были получены оптимальные решения, число испытаний при которых были получены решения отличающиеся от оптимальных менее чем на 5%, и число испытаний, при которых решения отличались от оптимального более чем на 5%.
Экспериментальные исследования показали, что наилучшим является следующее сочетание управляющих параметров: Рм=0.2, Рк=0.4.
На основе обработки экспериментальных исследований была построена зависимость качества решений от числа генераций.
В качестве аналога для сравнения выбран алгоритм WRST [7], основанный на последовательном построении взвешенных деревьев Штейнера. В алгоритме WRST также как и в рассмотренном в статье, каждая цепь представляется в виде связывающего дерева, построенного алгоритмом Прима, на основе которого последовательно строится дерево Штейнера с учетом веса ребер и динамически изменяющейся в процессе построения среды (коммутационного поля).
В таблице 1. представлены результаты сравнения экспериментальных данных с аналогом для пяти примеров.
В колонках F приводятся усредненные значения критерия F для генетического алгоритма (ГА) и для алгоритма WRST.
В колонке å L приводится суммарная длина, а в колонке t время работы алгоритма.
Как видно из таблицы генетический алгоритм обеспечивает более качественное решение, причем время решения на 10-40% меньше.
Сравнение с алгоритмами, использующими идею волнового алгоритма Ли, не проводилось, так как они дают худшие результаты, чем WRST[83].
Таблица 1.
| № | F | å L | T | |||
| WRST | WRST | WRST | ||||
| 1 | +2 | 0 | 4212 | 4570 | 33 | 37 |
| 2 | +3 | 0 | 3870 | 4610 | 31 | 34 |
| 3 | +1 | -2 | 5180 | 5900 | 57 | 69 |
| 4 | +3 | +1 | 4256 | 4570 | 59 | 61 |
| 5 | +2 | 0 | 3650 | 4220 | 29 | 34 |
5. Заключение
Приведена формулировка задачи глобальной трассировки. Определены перспективные критерии оптимизации. Разработана структура хромосомы, принципы ее кодирования и декодирования, использующие знания о задаче глобальной трассировки, исключающие возникновение неэффективных решений и повышающих скорость проектирования. Модернизированы и реализованы новые механизмы генетических процедур кроссинговера, мутации, смены популяций. Разработан генетический алгоритм глобальной трассировки на базе новых структур хромосом и модифицированных генетических процедур. Проведены экспериментальные исследования генетического алгоритма глобальной трассировки. Определены оптимальные сочетания значений управляющих параметрами М, Т, Рм, Рк. Проведено сравнение с аналогом показавшее, что разработанный алгоритм позволяет сократить сроки проектирования на 10-40%.
Список литературы
J.Soukup. Fast wise router .Proceedings of 15th Design Automation Conference, pages 100-102 ,1972.
J.Heisterman and T.Lengauer .The efficient solution of integer programs for hierarchical global routing . IEEE Transactions on Computer-Aided Design, CAD 10(6): 748-753, Jane 1991.
C.Chang , M.Sarrafzadeh ,and C.K. Wong .A powerful global router :Based on sterner min-max trees .Proceedings of IEEE International Conference on Computer-Aided Design, pages 2-5 , November 7-10 1989.
S.Burman , H .Chen ,and N. Sherwani . Improved global routing using l- geometry .Proceedings of 29th Annual Allerton Conference on Communications , Computing , and Control .October 1991 .
J.M. Ho , G. Vijayan , and C. K . Wong . A new approach to the rectilinear Sterner tree problem . IEEE Transactions on Computer -Aided Design , 9(2): 185-193 , February 1985 .
Селютин В.А. Автоматизированное проектирование топологии БИС .-М.:Радио и связь , 1983,-112 с .C.Chiang, M.Sarrafradeh, C.K.Wong. A Weighted-Steiner-Tree-Based Global Router, Manuscript, 1992.


