Реферат: Элементы теории устойчивости

Методы А. М. Ляпунова по исследованию устойчивости.

            Методы исследования были разделены Ляпунов на две категории.

            В первом случае устойчивость или неустойчивость разрешается на основании непосредственного исследования уравнений возмущенного движения. При этом требуется конкретное определение общего или частного решения системы уравнений возмущенного движения. Однако это удается лишь в очень редких случаях, поскольку в настоящее время неизвестны регулярные методы решения нелинейных дифференциальных уравнений.

            Во втором случае решения системы уравнений возмущенного движения вообще не требуется. Метод состоит в составлении определенной функции L, зависящей от t; x1,x2,...xn, с особыми свойствами, так называемой функции Ляпунова, из поведения которой и поведения ее производной по времени в окрестности нуля можно сделать вывод об устойчивости или неустойчивости движения.

            Положения об устойчивости по методу функции Ляпунова здесь подробно рассматриваться не будут. С ними при желании можно ознакомиться в соответствующей литературе. Ограничимся вытекающими из них положениями об устойчивости линеаризованной системы, которых вполне достаточно для исследования в большинстве практически интересных случаев. Эти положения справедливы стационарных, установившихся состояний или движений, при которых функции Xν в уравнениях (7) или функции Xν в уравнениях (11) не зависят от времени t. Прежде чем приводить положения об устойчивости рассмотрим вкратце для лучшего понимания вопрос об устойчивости непосредственно линейной системы, исследование которой возможно без применения функции Ляпунова, более простым способом.

Положения Ляпунова об устойчивости линеаризованной системы.

Рассмотрим линейную  систему дифференциальных уравнений (12). Метод определения решений этой системы хорошо известен из общей теории линейных дифференциальных уравнений с постоянными коэффициентами. А именно, будем искать решения в виде:

где  Cν и λ- константы, подлежащие определению. Тогда после сокращения на e­­­­λt ≠0 получим систему алгебраических уравнений:

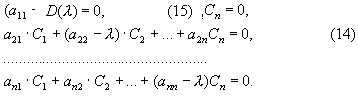            Эта система уравнений при определении неизвестных коэффициентов Cν имеет нетривиальное, отличное от нуля решение, если определитель ее D(λ) равен нулю:

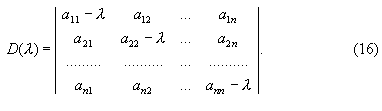где

 Уравнение (15) представляет собой характеристическое уравнение системы дифференциальных уравнений (12) и является алгебраическим уравнением n-ой степени относительно λ:

где a­ν-постоянные коэффициенты характеристического уравнения, которые определяются коэффициентами aνi определителя (16) и системы (12). Уравнение (17) имеет в общем случае n различных комплексных корней:

где λi’, λi’’-соответственно действительные и мнимые части корней, а j-мнимая единица. Тогда общее решение системы (12) будет равно сумме всех частных решений (13) и может быть представлена в виде:

где постоянные Cνi определяются конкретными начальными условиями задачи, т. е. начальными возмущениями системы.

            На основании общего решения задачи о возмущенном движении линейной системы (12), полученного в виде соотношений (19), (18) можно сделать следующие выводы об устойчивости.

1. Если вещественные части всех корней характеристического уравнения отрицательны

то  выполняется условие (6). В этом случае линейная система асимптотически устойчива.

2. Если среди корней характеристического уравнения найдется хотя бы один с положительной вещественной частью

то в решении xν­(t) (19) будет присутствовать хотя бы одно слагаемое, которое с течением времени будет неограниченно нарастать. В этом случае линейная система неустойчива.

3. Если среди корней характеристического уравнения нет корней с положительной вещественной частью (21), однако имеются корни с вещественными частями, равными нулю

то выполняется условие (5). В этом случае линейная система просто устойчива.

Положения Ляпунова об устойчивости исходной нелинейной системы.

Обратимся теперь к нелинейной системе (7). А.М. Ляпунову удалось показать, что на основе анализа линеаризованной системы (12) можно сделать довольно существенные выводы и о поведении исходной нелинейной системы. Сформулируем следующие основные положения Ляпунова, которые примем без доказательств.

1. Если все корни характеристического уравнения системы первого приближения имеют отрицательные вещественные части (20), то невозмущенное движение исходной нелинейной системы устойчиво в обычном смысле (4), (5).

2. Если среди корней характеристического уравнения системы первого приближения найдется хотя бы один с положительной вещественной частью (21), то невозмущенное движение исходной нелинейной системы неустойчиво.

3. Если характеристическое уравнение системы первого приближения не имеет корней с положительной вещественной частью, однако имеет такие, у которых вещественные части равны нулю (22), то ответ на вопрос об устойчивости или неустойчивости исходной нелинейной системы дан быть не может на основании линейного анализа. Необходимо более глубокое нелинейное исследование.

Т. о., два первых положения описывают так называемые «некритические» случаи, в которых можно дать ясный ответ на вопрос об устойчивости нелинейной системы на основании исследования системы первого приближения. Третье положение соответствует «критическому» случаю, когда определенный вывод об устойчивости или неустойчивости нелинейной системы  можно сделать только при дополнительном исследовании уравнений с учетом нелинейных слагаемых более высоких порядков малости, чем первый.

Методы анализа устойчивости линейных и линеаризованных систем.

Итак, для определения устойчивости такой системы необходимо определение всех корней ее характеристического уравнения до единого. Однако в системах высокого порядка вычисление корней весьма затруднительно. При этом часто приходится прибегать к численным методам, что еще более затрудняет задачу.

Чтобы избежать указанных трудностей и не вычислять вообще корней характеристического уравнения был разработан ряд методов, так называемых критериев устойчивости. При их помощи можно определить характер устойчивости или неустойчивости системы, не вычисляя корней характеристического уравнения.

В настоящее время известно множество критериев устойчивости, позволяющих решать задачу при различных, конкретных условиях. Таковы алгебраический критерий Гурвица, критерий Рауса, частотный критерий Найквиста  с различными дальнейшими модификациями, например, Михайлова, и др. Несмотря  на формальное различие перечисленных критериев друг от друга, по сути все они основаны на известной теореме теории функций комплексного переменного, а именно, теореме Коши относительно числа нулей и полюсов функции, аналитической в заданной области.

Поскольку критерии устойчивости обстоятельно изложены в литературе, в дальнейшем  ограничимся подробным рассмотрением лишь двух из множества критериев: Гурвица и Рауса.

 

Необходимое условие устойчивости.

            Пусть характеристическое уравнение линейной или линеаризованной системы уравнений (12) возмущенного движения представлено в виде (17), причем, для определенности

В противном случае уравнение умножают на –1.

            Нетрудно доказать следующее необходимо условие устойчивости. Для устойчивости линейной системы любого порядка необходимо, но не достаточно, чтобы все коэффициенты характеристического уравнения были положительными.

            Иными словами, если линейная система устойчива, то коэффициенты ее характеристического уравнения положительны, но не наоборот.

            При доказательстве положим, что система заведомо устойчива, т. е. все корни ее характеристического уравнения имеют отрицательные вещественные части:

Страницы: 1, 2, 3, 4