Реферат: Дискретные цепи

 (2.18)

Для периодических дискретных сигналов корреляционная функция и энергетический спектр связаны формулами ДПФ

. (2.19)

Отсюда получаются расчётные формулы энергии периодических дискретных последовательностей

, (2.20)

что соответствует равенству Парсеваля для дискретных периодических сигналов. Корреляционная функция таких сигналов определяется по формуле круговой свёртки

.

Расчет энергии дискретного сигнала можно выполнить при необходимости, применяя равенство Парсеваля относительно Z - изображений сигнала и его инверсной копии (теорема энергий)

, (2.21)

где  - Z - изображение корреляционной функции.

Уместно заметить, что применительно к случайным сигналам корреляционная функция чаще определяется формулой с весовым множителем , т.е.

,

соответственно для энергетического спектра

,

что приводит к результату, при котором среднее значение случайной величины с ростом N сходится к постоянной величине.

Свертка сигнала с инверсной копией другого сигнала называется взаимной корреляцией этих сигналов.

Расчёт энергии сигнала в дискретной цепи.

В любой точке дискретной цепи энергию сигнала можно вычислить по известному сигналу или по корреляционной функции сигнала в этой точке. Корреляционную функцию сигнала в некоторой точке цепи можно определить не только по известному сигналу, но и по известной корреляционной функции входного сигнала и импульсной реакции

, (2.22)

где  - корреляционная функция сигнала на входе цепи,

 - корреляционная функция импулсного отклика в данной точке,

 - условный знак свёртки.

Докажем равенство (2.22).

.

В этом выражении в силу линейности цепи сигналы можно сочетать различными способами. Поэтому

,

что доказывает справедливость (2.22). Следовательно

. (2.23)

Автокорреляционная функция является чётной функцией, поэтому применяя круговую свёртку (2.22), периоды  и  необходимо выровнять с таким расчетом, чтобы сохранить чётный характер этих функций.

Пример. Определить энергию сигнала на выходе цепи, если

x(nT) = {0,5; 0,5}, h(nT) = {1,0; 0,5}.

Решение.

1. Расчет во временной области.

Определяем сигнал на выходе цепи по формуле круговой свёртки

Отсюда .

2. Расчёт в частотной области.

Вначале необходимо определить отсчёты спектра сигнала по формуле прямого ДПФ

.

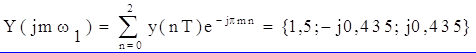Отсюда, согласно равенству Парсеваля,

.

3. Расчёт по формуле (2.23).

Определяем корреляционные функции  и .

Следовательно, .

увеличивая период  и  до N=5, получаем

, .

На рис.(2.9,а) показана периодическая последовательность  до увеличения периода, на рис. (2.9,б) - после увеличения периода .

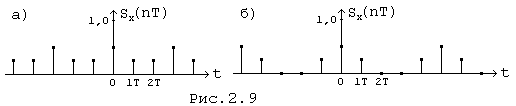
Согласно (2.22)

.

Отсюда .

В заключении рассмотрим важный часный случай применения формулы (2.23).

Для случайных сигналов с нулевым средним

, (2.24)

где  - дисперсия случайного сигнала x(nT).

Отсюда, учитывая (2.23),

.

Следовательно

, (2.25)

Формула (2.25) применяется, в частности, для расчёта шумов квантования в цифровых цепях .

Секционирование.

Реальные сигналы могут иметь значительную протяжённость во времени, поэтому обработка таких сигналов на ЭВМ осуществляется посекционно. Расчёты по каждой секции  выполняются по формуле круговой свёртки

,

где h(nT) - импульсная характеристика, определяющая способ обработки сигнала .

Каждая секция  совмещается с предидущей секцией с учётом сдвига между секциями входного сигнала .

Применяются два основных метода секционирования: метод перекрытия с суммированием и метод перекрытия с накоплением.

1. Метод перекрытия с суммированием.

Сигнал x(nT) разбивается на секции длиной L. Отсюда- длина секции ,  - длина секции ,  - длина  .

Длина секции  больше длины секции  на . Поэтому смежные секции выходного сигнала  перекрываются на интервале длиной . На интервале перекрытия необходимо выполнить арифметические операции по суммированию отсчётов.

2. Метод перекрытия с накоплением.

Сигнал x(nT) разбивается на секции длиной L. Затем каждая секция наращивается слева участком предидущей секции длиной  . Поэтому

 - длина ,  - длина ,  - длина .

Искусственное удлинение каждой секции приводит к тому, что первые и последние  отсчётов секции  являются ложными и поэтому отбрасываются. Оставшиеся L отсчётов каждой секции, являются истинными, поэтому смежные секции  совмещаются без перекрытия и без зазора.

Пример. Осуществить посекционную обработку сигнала

x(nT) = { 1,0; 0,5 }, если h(nT)= { 1,0; 0,5 }.

Решение.

Применим метод перекрытия с накоплением.

Пусть L = 1. Отсюда ;

, поэтому после искусственного удлинения секций:

.

Выравниваем периоды сигналов для применения круговой свёртки:

N = N1 + N2- 1 = 3. Следовательно x0(nT)= {0; 0,4; 0}, x1(nT)= {0,4; 0,8; 0}, x2(nT)= {0,8; 0; 0} После свёртки по каждой секции и отбрасывания  отсчётов получаем:  отсюда

y(nT)= {0,4; 1,0; 0,4}.

Метод перекрытия с накоплением получил преимущественное распространение, поскольку здесь не требуется проведения дополнительных арифметичкских операций после обработки каждой секции.