Реферат: Численные методы и их реализация в Excel

Функция спроса

Q=50e-3

Функция предложения

Q=3p-4e

0<p<20

Глава 2. Матричная алгебра

По   мнению   крупнейшего   экономиста   нашей   эпохи В.В.Леонтьева. «Дифференциальное исчисление и элементарная алгебра - два традиционных инструмента экономиста-математика заменяются . или, по крайней мере дополняются матричной алгеброй.»4Матричная алгебра тесно связана с линейными функциями и с линейными ограничениями в связи с чем находит себе применение в различных экономических задачах:

• в эконометрике, для оценки параметров множественных линейных регрессий;

• при решении задач линейного программирования;

• при макроэкономическом моделировании и т.д. Особое отношение к матричной алгебре в экономике появилось после       создания моделей типа «Затраты - Выпуск», где с помощью матриц технологических коэффициентов объясняется уровень производства в каждой отрасли через связь с соответствующими уровнями во всех прочих отраслях.

Электронная таблица EXCEL имеет ряд встроенных функций для работы с матрицами:

ТРАНСП - транспонирование исходной матрицы - вычисление определителя квадратной матрицы

МОПРЕД- вычисление определителя  квадратной матрицы

МОБР - вычисление матрицы обратной к данной - нахождение матрицы, являющейся произведением двух матриц.Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц и умножения (деления) матрицы на число.                         Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических,    они располагаются в полном алфавитном перечне.

МУМНОЖ- нахождение матрицы, являющейся произведением двух матриц.

Кроме того возможно выполнение операций поэлементного сложения (вычитания ) двух матриц  и умножения (деления) матрицы на число.

Все вышеперечисленные функции вызываются через мастер функций и хотя относятся к разделу математических , они располагаются в полном алфавитном перечне.

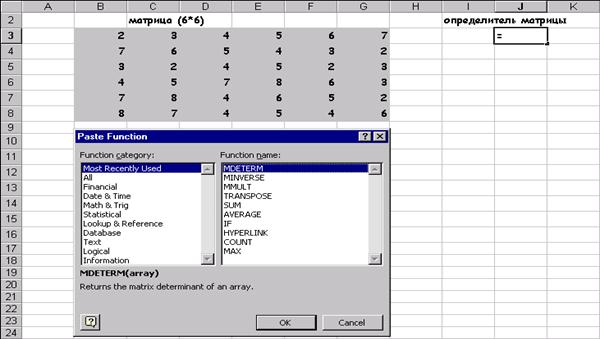
2.1 Определитель матрицы

Для вычисления определителя матрицы сформируем лист электронной таблицы, как показано на Рис.9. Место записи вычисленного определителя матрицы определяется  местоположением табличного курсора.

Пусть на листе электронной таблицы сделаны все предварительные действия, т.е введена матрица, над которой будут производиться действия и определено место записи результата.

Следующим шагом  вызывается  мастер функций  рис10., левое окно которого содержит перечень разделов , а правое алфавитный список функций, составляющих  данный раздел.

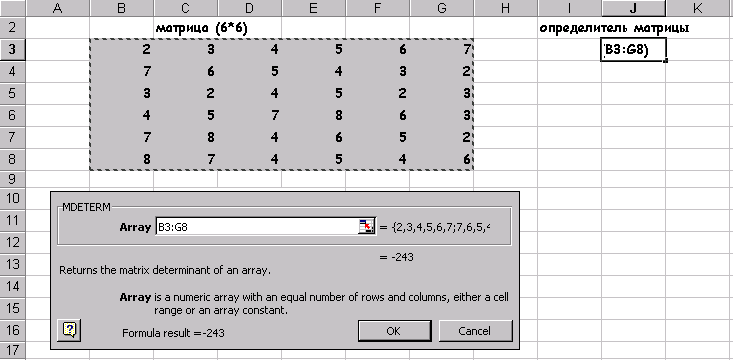
В левом окне  выбираем раздел  -« Полный алфавитный перечень «, а в правом МОПРЕД , В появившемся  диалогом окне  Рис11. Следует указать левый верхний  и через двоеточие  правый нижний  адреса матрицы, (или обвести интересующую нас матрицу, при нажатой клавиши  мыши, штриховой линией, что автоматизирует процесс определения адресов местоположения  матрицы на листе ЭТ) Рис.11

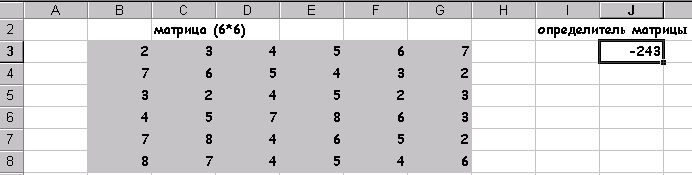
Щелкнув   на кнопке   Готово получим значение определителя, размещенного в клетке С10. Его значение равно 1 Нахождение определителя - это единственное действие .над матрицей, которое дает в результате число, остальные матричные функции в результате своих действий дают матрицы и , это,следует, учитывать при подготовке на листе ЭТ места для размещения результата.

2.2 Умножение матриц

В качестве примера рассмотрим умножение двух матриц.  Пусть надо умножить матрицу А(5*4) на матрицу В(4*3). это умножение возможно, так как число столбцов матрицы А совпадает с числом строк матрицы В . результатом будет матрица С(5*3).

Перед вызовом функции умножения матриц сформируем лист ЭТ, так как показано на Рис.12

Затем выполним следующую последовательность действий:

1.Зададим матрицу А

2. Зададим матрицу В

3 Отметим место для матрицы   С7                       

              4. Обратимся к мастеру функций , найдем в полном алфавитном  перечне функцию МУМНОЖ и выполним постановку задачи так. Как показано на Рис. 13

В качестве массива 1 указывается  диапазон адресов  матрицы А, а в качестве массива 2- диапаон адресов  матрицы В.

Щелкнуть  в на кнопке Готово получим в клетке, где присутствует знак равенства, полную запись функции умножения. Для получения результата необходимо нажать клавиши Shift/Ctrl/Enter одновременно8

7В выделенном под результат месте ЭТ поставить знак равенства.

8Все матричные функции, за исключением вычисления определителя. требуют заключительного одновременного нажатия клавиш Shift/Ctrl/Enter

На Рис 15 показан результат умножения после нажатия клавш Shift/Ctrl/Enter, а в строке формул стоит выражение в "фигурны скобках, {3*B4:D6} что является признаком выполнения матрично операции

Сложение матриц

Для сложения двух матриц одинаковой размерности10 следует выполнить следующую  последовательность действий. . Задать две исходных матрицы. . Отметить место для матрицы - результата. • . В выделенном под результат месте ЭТ поставить знак равенства и записать сумму так. как показано на Рис. 16. . -Завершить выполнение работы нажатием клавиш Shift/Ctrl/Enter, Рис.17".

Фигурные скобки в строке формул {В4:D6+F4:H6}-признак выполнения матричной операции

 

Задание 3

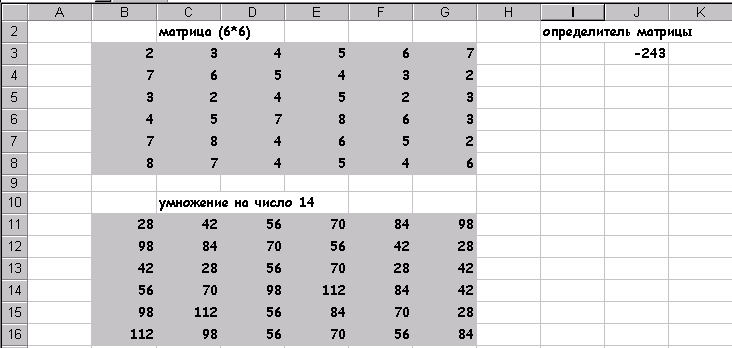
 Найти определитель матрицы  В (6*6):. умножить матрицу на 14.

Умножение на число 14

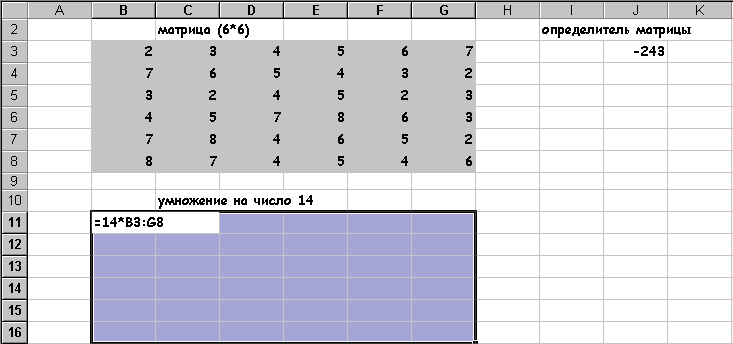
результат:

 

 

 

 

 

 

 

 

 

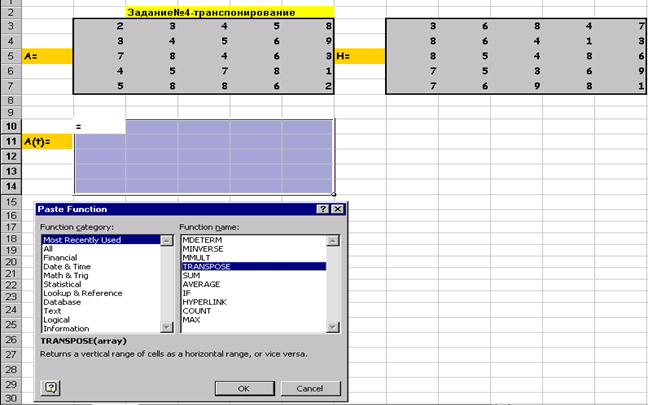
Задание 4

 

Транспонирование матрицы А :

 

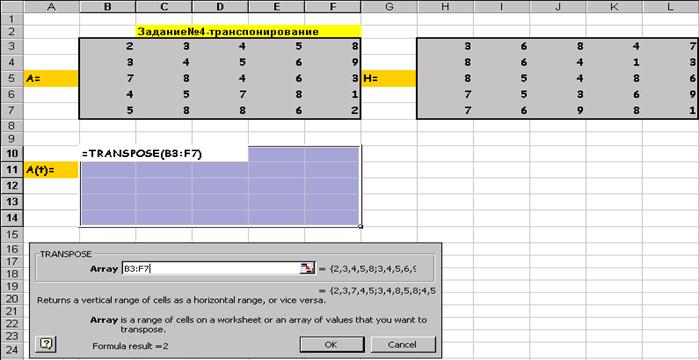
После нажатия Shift/Ctrl/Alt:

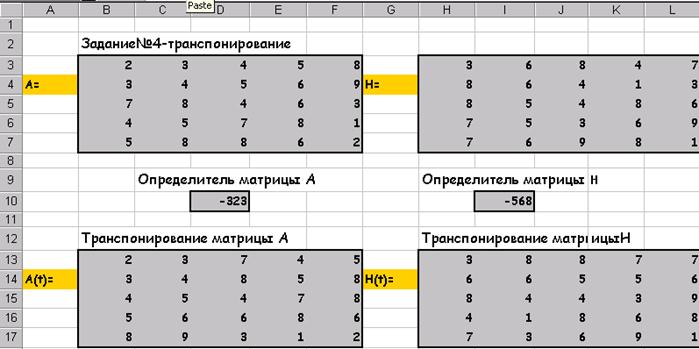
Умножение матриц  А на H(t):

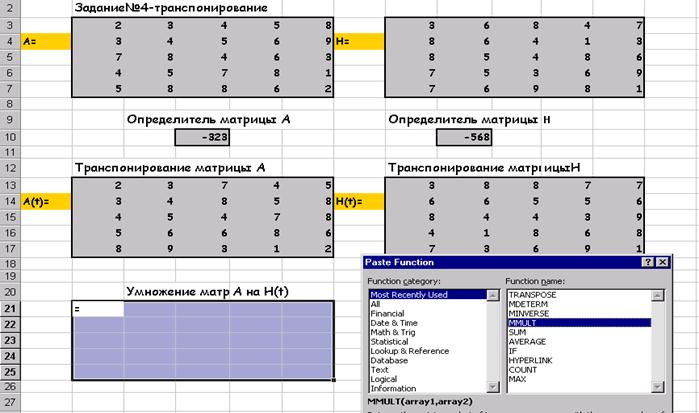
После нажатия на ОК:

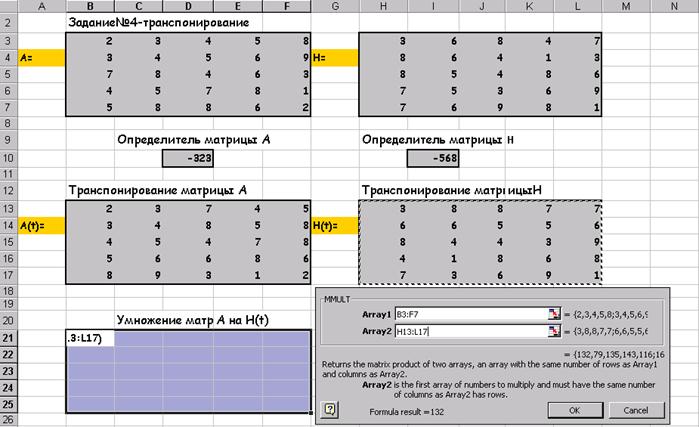
Вычитание матриц AH(t)  и HA(t):

 

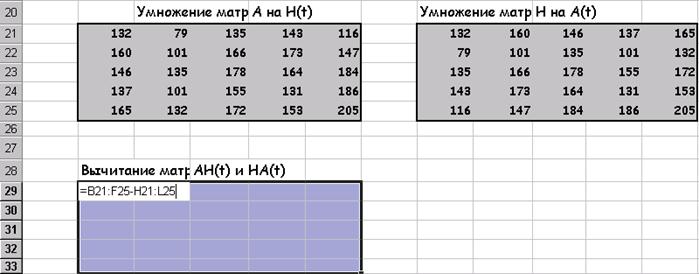
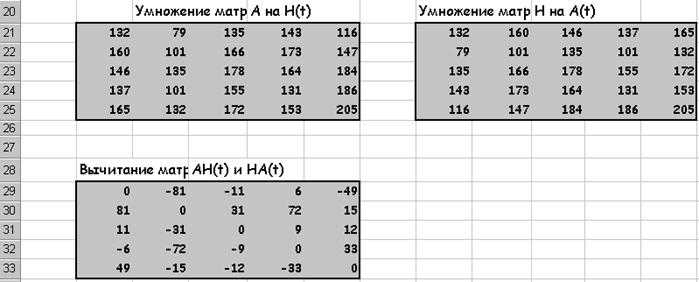
2.6 Система линейных алгебраических уравнений

Решение Система линейных алгебраических уравнений всегда занимало  математиков  и для решения было разработано немало численных методов, подразделяющихся на прямые ( Гаусса, Кремера)  и итерационные (простых итераций , Зейделя ,верхних релакций… )

                    EXCEL задача получения решение СЛАУ решаются с помощью вышеописанных матричных функций, для чего исходную систему надо представить в виде матричного уравнения.

Рассмотрим последовательность  действий  для получения решение СЛАУ на конкретном примере.

Задание 5

Найти  решение системы линейных алгебраических уравнение и сделать проверку.

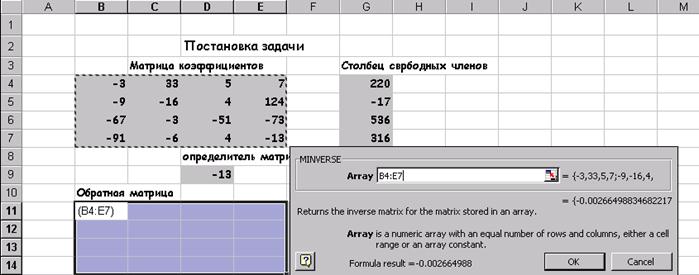
Для того, чтобы  система (5) имела единственное решение необходимо и достаточно, чтобы определить системы, составленный из коэффициентов при переменных  х,х,х,х, не был равен нулю.

          Рассчитаем определить системы пользуясь функцией МОПРЕД. Рассчитанное значение  определителя системы равно 1662723продолжать процесс поиска решения.

                        Из линейной алгебры известна матричная запись системы уравнений и матричное преставление решения.

Перепишем систему уравнений (5):

Тогда матричное решение уравнения выглядит так:

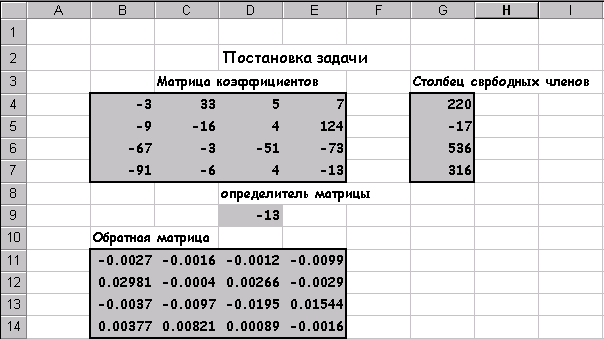
Результат, указанный  на рис18 можно   получить,  выполнив  следующие  действия:

1.   Вычислить определитель и выяснить  имеет ли система  единственное решение.

2.    Вычислить матрицу  обратную к исходной.

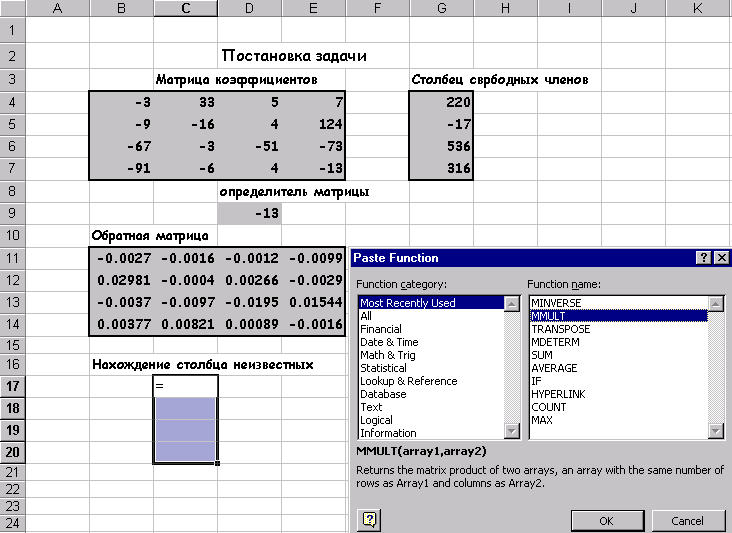
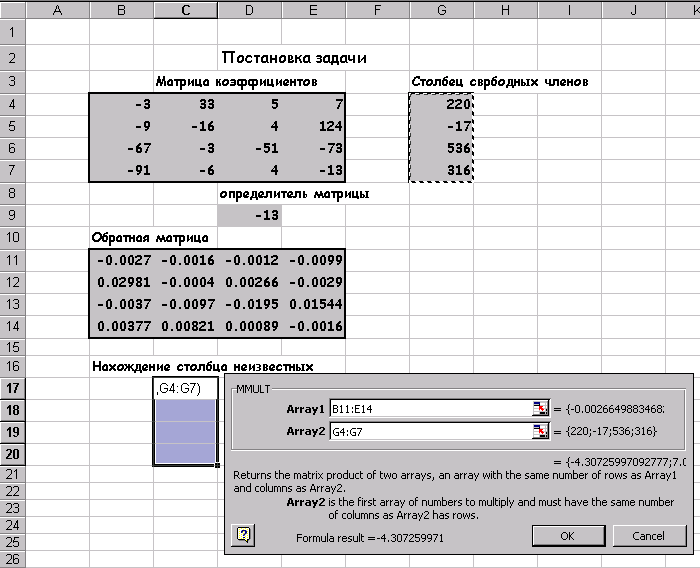
3.   Найти произведение обратной матрицы и вектор столбца свободных членов.

Страницы: 1, 2, 3