 Лабораторная работа: Оцінка трудомісткості алгоритму
Лабораторная работа: Оцінка трудомісткості алгоритму
Лабораторная работа: Оцінка трудомісткості алгоритму
Міністерство освіти і науки, молоді та спорту України
Тернопільський національний технічний університет ім. І.Пулюя
Кафедра комп’ютерних систем та мереж
Звіт
до лабораторної роботи №4
на тему Оцінка трудомісткості алгоритму
з дисципліни Комп’ютерні системи
Виконав:
Студент групи СІ 22
Никорчук Володимир
Перевірив:
Хомів Богдан Арсенович
Тернопіль 2011
Частина 1. Засвоєння засобів аналізу трудомісткості обчислювальних алгоритмів
Короткі теоретичні відомості:
Задача, що підлягає вирішенню на ПК, може бути охарактеризована кількістю даних, складністю алгоритму та його трудомісткістю. Під трудомісткістю алгоритму розуміється кількість обчислювальної роботи,необхідної для його реалізації. Трудомісткість характеризує витрати часу для реалізації алгоритму на деякій сукупності технічних засобів. Звичайно, трудомісткість оцінюється кількістю процесорних операцій та операцій введення-виведення. В загальному випадку, трудомісткість алгоритму є випадковою величиною, що залежить від вхідних даних. Тому, трудомісткість алгоритму може бути визначена тільки наближено, в термінах теорії ймовірностей: математичним сподіванням, дисперсією і т. д.
Трудомісткість алгоритму в першому наближенні може бути охарактеризована набором параметрів:
ϴ - середня кількість процесорних операцій, необхідних для однієї реалізації алгоритму;
N1, N2 ,… NH – середня кількість запитів до файлів за один прогін програми;
L1, L2 ,… LH - середня кількість інформації, що передається за одне звернення до файлів F1, F2 ,… FH .
При необхідності набір параметрів, що характеризують трудомісткістю алгоритму може бути доповнений. Вхідна інформація для розрахунку трудомісткості алгоритму може бути одержана з блок-схеми алгоритму.
Для розрахунку трудомісткості алгоритму необхідно знати ймовірності переходів з логічних вершин при одиничному значенні логічної умови. Якщо відповідну ймовірність визначити через p, тоді ймовірність виходу з логічної вершини при нульовому логічному значенні умови, що перевіряється буде дорівнювати l-p . Для подальших розрахунків схему алгоритму раціонально зображати в вигляді графа алгоритму. Для цього пропонується перенумерувати всі оператори схеми алгоритму. У логічних операторів замість логічних умов «1» і «0» будемо записувати відповідну даному виходу ймовірність. Ймовірність виходу з операторної вершини дорівнює 1. Граф алгоритму можна істотно спростити, якщо трудомісткість виконання логічних вершин незначна в порівнянні з трудомісткістю виконання операторних вершин. Тоді стани, що відповідають логічними вершинами, можна злити з станами, що випереджають відповідні операторні вершини.
Хід роботи:
1. Побудова блок-схеми за логічною схемою алгоритмів.
Поч. X1↑1
А![]() В
X2↑2
С X3↑3
В
X2↑2
С X3↑3
![]() Е
X4↑4
К
Е
X4↑4
К ![]() М
Кін.
М
Кін.
Блок-схема даного алгоритму зображена на рис.1.
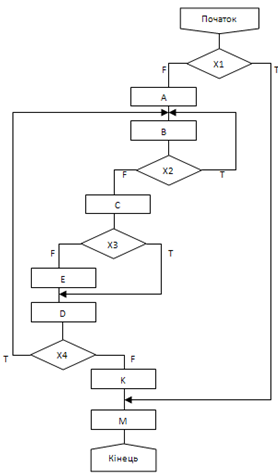
Рисунок 1
2. Побудова графа даного алгоритму з отриманої вище блок-схеми, що показано на рис.2.
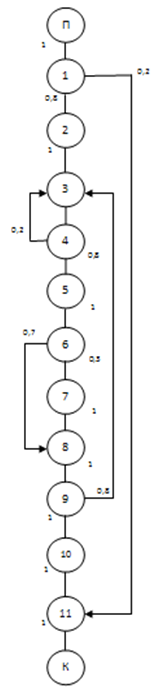
Рисунок 2
3. Мінімізація графа даного алгоритму, що показано на рис. 3.
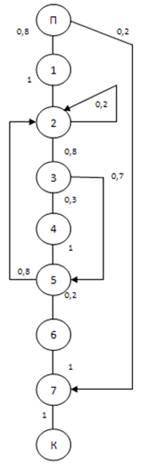
Рисунок 3
4. Подання графа у вигляді стохастичної матриці зображено в таблиці1.
алгоритм граф трудомісткість excel
Таблиця1
| S1 | S2 | S3 | S4 | S5 | S6 | S7 | Sk | |
| S0 | 0.8 | 0.2 | ||||||
| S1 | 1 | |||||||
| S2 | 0.2 | 0.8 | ||||||
| S3 | 0.3 | 0.7 | ||||||
| S4 | 1 | |||||||
| S5 | 0.8 | 0.2 | ||||||
| S6 | 1 | |||||||
| S7 | 1 |
5. Розв`язання системи алгебраїчних рівнянь, рішення яких дає середнє число запитів до операторів, що показано в таблиці 2.
Таблиця 2
| n0= | 1 | n0= | 1 |
| n1= | 0.8n0 | n1= | 0.8 |
| n2= | 1n1+0.2 n2+0.8 n5 | n2= | 5 |
| n3= | 0.8n2 | n3= | 4 |
| n4= | 0.3n3 | n4= | 1.2 |
| n5= | 0.7n3+1n4 | n5= | 4 |
| n6= | 0.2n5 | n6= | 0.8 |
| n7= | 0.2 n0+1n6 | n7= | 1 |
6. Знаходження середньої кількості процесорних операцій за допомогою програми Microsoft Excel показана на рис.4.
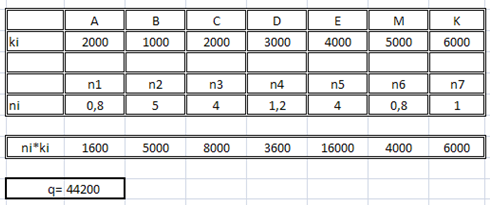
Рисунок 4
7. Знаходження кількості звернень до файлів та довжин за допомогою програми Microsoft Excel зображено на рис.5.
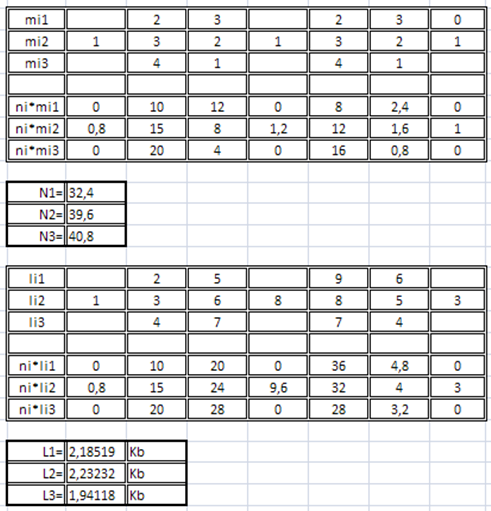
Рисунок 5
Частина 2. Компіляція програми
Операційна система Linux має багато вбудованих компіляторів, практично під кожну мову програмування високого рівня. Два найбільш поширені компілятори – це gcc та g++ для мов програмування С та С++ відповідно. В даній лабораторній роботі я використовував компілятор g++, з допомогою якого скомпілював програму, що обчислює числа Фібоначчі. Ця програма складається з двох файлів lab.cpp та fib.h. Перший містить головну функцію програми і слугує для вводу виводу чисел. Другий проводить математичні операції з числами. Результат виконання програми об’єднується і записується в один об’єктний файл lab1. Щоб зібрати всі файли в один, потрібно використати ключ –о, наприклад: g++ lab.cpp fib.h –o lab1. Виконуємо отриманий файл за допомогою команди ./lab1 .
Нижче наведено лістинг програми та скріншот, який показує результат виконання.
Лістинг 2.1 lab.cpp
#include <iostream>
#include "fib.h"
using namespace std;
int main()
{
long n;
cout<<"Enter the fibonacci number:"; cin>>n;
cout<<"The "<<n<<" number of fibonacci is:"<<fibonacci(n)<<endl;
return 0;
}
Лістинг 2.2 fib.h
long fibonacci ( long n)
{
if ( n == 0)
{
return 0;
}
else if ( n == 1 )
{
return 1;
}
Else return fibonacci( n -1) + fibonacci(n-2);}
Висновок
На даній лабораторній роботі я засвоїв засоби аналізу трудомісткості обчислювального алгоритму, а також навчився компілювати програми в консольному режимі Linux.


