Лабораторная работа: Исследование точности численного интегрирования
Лабораторная работа: Исследование точности численного интегрирования
Министерство общего и профессионального образования РФ.
Уральский государственный технический университет – УПИ
Кафедра “Технология и средства связи”
"Исследование точности численного интегрирования"
"Research of Accuracy of Numerical Integration"
Отчет
по лабораторной работе
дисциплины
"Информатика",
третий семестр
Преподаватель: Болтаев А.В.
Студенты: Степанов А.Г
Черепанов К.А.
Группа: Р-207
Екатеринбург
2000
Содержание
1. Задание исследования.................................................................. 3
2. Подробное описание задачи и способы ее решения................... 3
3. Результаты исследований............................................................. 4
4. Сравнение результатов.............................................................. 12
5. Список библиографических источников................................... 13
6. Текст программы........................................................................ 13
Задание исследования
Провести исследование внутренней сходимости численного интегрирования методом Симпсона и трапеций различных функций, задаваемых с помощью языка С.
Подробное описание задачи и способы ее решения
Необходимо провести исследования так называемой внутренней сходимости численного интегрирования методами Симсона и трапеций различных функций, задаваемых с помощью функций языка С. Предполагается, что отрезок интегрирования [a,b] разбит на n равных частей системой точек (сеткой).
Контроль внутренней сходимости заключается в циклическом вычислении приближенных значений интеграла для удваимого по сравнению со значением на предыдущем прохождении цикла числа n. Отношения абсолютной величины разности этих значений к абсолютной величине предыдущего приближенного значения принимается в качестве критерия достижения точности интеграла.
Построить зависимости количеств итераций от различных величин критерия точности.
Построить обратные зависимости критерия точноти от количества итераций.
Повторить все вышеуказанные исследования для случая, когда при вычислении критерия точности разность значений интеграла относится не к предыдущему значению, а к точному значению аналитически вычисленного интеграла.
Исследовать влияние увеличения верхнего предела интегрирования на точность (при прочих неизменных условиях)
Метод трапеций
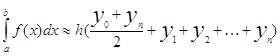, где
Метод Симпсона
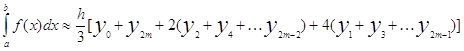, где
Результаты исследований
Таблица и график зависимости количества итераций от различных значений критерия точности
Для 
| Критерий точности | Количество итераций |
| -0,1676631 | 14 |
| -0,1518916 | 16 |
| -0,0046931 | 12 |
| -0,0026531 | 11 |
| -0,0002639 | 10 |
| -0,0001709 | 2 |
| -0,0001297 | 9 |
| -0,0000557 | 3 |
| -0,000025 | 8 |
| -0,0000198 | 4 |
| -0,0000096 | 5 |
| -0,0000038 | 6 |
| 0 | 15 |
| 0,0000052 | 7 |
| 0,071089 | 13 |
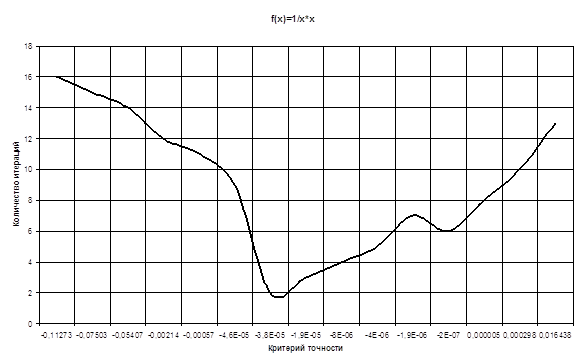
| Критерий точности | Количество итераций |
| -0,1127271 | 16 |
| -0,0750288 | 15 |
| -0,0540677 | 14 |
| -0,0021415 | 12 |
| -0,0005711 | 11 |
| -0,0000458 | 9 |
| -0,0000381 | 2 |
| -0,0000191 | 3 |
| -0,000008 | 4 |
| -0,000004 | 5 |
| -0,0000019 | 7 |
| -0,0000002 | 6 |
| 0,000005 | 8 |
| 0,0002983 | 10 |
| 0,0164377 | 13 |
 |
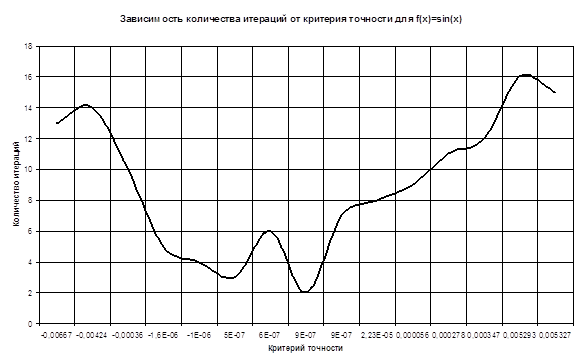
| Критерий точности | Количество итераций |
| -0,0066709 | 13 |
| -0,0042367 | 14 |
| -0,0003561 | 10 |
| -0,0000016 | 5 |
| -0,000001 | 4 |
| 0,0000005 | 3 |
| 0,0000006 | 6 |
| 0,0000009 | 2 |
| 0,0000009 | 7 |
| 0,0000223 | 8 |
| 0,000056 | 9 |
| 0,0002782 | 11 |
| 0,0003474 | 12 |
| 0,005293 | 16 |
| 0,0053267 | 15 |
 |
