Курсовая работа: Уравнение Лапласа, решение задачи Дирихле в круге методом Фурье

Координаты х, у, z, допускающие решения с - разделенными переменными. Трехмерное уравнение Пуассона, как и трехмерное уравнение Лапласа, часто встречается в теории тепло - и массопереноса, гидро - и аэромеханике, теории упругости, электростатике и других областях механики и физики. Оно описывает стационарное распределение температуры при наличии источников ( или стоков) тепла в рассматриваемой области.

Компонента / ZQO должна даваться скалярным решением трехмерного уравнения Лапласа.

Компонента / IQO должна даваться скалярным решением трехмерного уравнения Лапласа.

Показать, что если ф ( г) - решение трехмерного уравнения Лапласа, то и ф ( г) Ц - 1 - также решение.

Задача в этом случае может быть решена классическим методом построения функций Грина для трехмерного уравнения Лапласа, но вследствие малости поперечных размеров капиллярной трубки по сравнению с длиной и высокой проводимости металла можно считать окружность поперечного сечения трубки эквипотенциальной с достаточной точностью в пределах разрешающей способности приборов. Поэтому целесообразно сразу принять допущение о цилиндрической симметрии объекта и решать задачу более просто с построением соответствующего интегро-дифференциального уравнения.

Задача в этом случае может быть решена классическим методом построения функций Грина для трехмерного уравнения Лапласа, но вследствие малости поперечных размеров капиллярной трубки по сравнению с длиной и высокой проводимости металла можно считать окружность поперечного сечения трубки эквипотенциальной с достаточной точностью в пределах разрешающей способности приборов. Поэтому целесообразно сразу принять допущение о цилиндрической симметрии объекта и решить задачу более просто с построением соответствующего интегро-дифференциального уравнения.

Сеточные модели используются для решения краевых задач, описываемых двух - или даже трехмерными уравнениями Лапласа, Гельмгольца или Фурье.

После растяжки вертикальной координаты в раз поставленная задача в общем случае сводится к решению трехмерного уравнения Лапласа для потенциала скорости ф и не имеет аналитического решения. Чтобы получить приближенную формулу для дебита горизонтальной скважины, в работе используется известный в подземной гидромеханике прием: трехмерная задача фильтрации заменяется двумя плоскими задачами.

Множество инженерных задач, связанных, в частности, с медленным стационарным обтеканием корпуса корабля, стационарной фильтрацией подземных вод, возникновением поля вокруг электромагнита, а также стационарного электрического поля в окрестности фарфорового изолятора или заглубленного в землю электрического кабеля переменного поперечного сечения, сводится к решению трехмерных уравнений Лапласа или Пуассона.

Такие функции называются гармоническими; из них нужно выбрать те, которые удовлетворяют граничным условиям задачи. Поэтому целесообразно создать возможно больший запас гармонических функций, различные сочетания которых, а часто и каждая в отдельности, могут соответствовать задачам, имеющим важное практическое значение. Наиболее простые частные решения уравнения Лапласа можно получить, предположив, что потенциал Ф зависит только от одной координаты. Такое предположение означает, что трехмерное уравнение Лапласа в частных производных распадается в некоторых системах координат на три одномерных дифференциальных уравнения, каждое из которых равно нулю. При этом можно руководствоваться первым следствием из теоремы единственности: электростатическое поле между двумя равнопотенциальными поверхностями и гармоническая функция, описывающая это поле, не изменяется, если эти поверхности сделать границами проводников, которым сообщены соответствующие потенциалы.

В заключение заметим, что развитая методика построения равномерно пригодного решения для задачи входа тонкого пространственного тела в жидкость ( разд. В частности, при наличии излома передней кромки методика непригодна. Так, на дозвуковом режиме входа пространственного тела в жидкость характеристики линейного ( внешнего) решения задачи имеют логарифмическую особенность в носике тела при стремлении к нему точки поля возмущенного течения по любому направлению. Поэтому внутренние переменные в этом случае необходимо вводить по всем трем декартовым координатам x y z, что приведет к внутренней задаче для трехмерного уравнения Лапласа с соответствующими краевыми условиями на поверхности пространственного тела в окрестности носика.

Однако остаются иные задачи, имеющие также весьма серьезное значение, которые отличаются вполне определенным пространственным характером. Так, если скважина, вскрывшая продуктивный песчаник, полностью не проходит сквозь него, то течение в той части песчаника, которая не вскрыта забоем скважины, будет иметь компонент скорости, направленный вверх и влекущий жидкость в скважину. По отношению к общим методам решения пространственных задач следует заметить, что все те методы, которые были рассмотрены нами в приложении к плоским системам, за исключением только одного из них, имеют свои аналоги в том случае, когда в систему включается третья координата. Только метод сопряженных функций не имеет своего аналога для случая трехмерного уравнения Лапласа. Все же для решения практических задач мы находим, что имеющиеся в нашем распоряжении методы вполне достаточны для получения искомых результатов. Численные методы решения - методы, заменяющие исходную краевую задачу дискретной задачей, содержащей конечное число N неизвестных, нахождение которых с соответствующей точностью позволяет определить решение исходной задачи с заданной точностью  ; N зависит от  и стремится к  при .

3.Уравнение Лапласа в случае пространственных переменных

 имеет вид

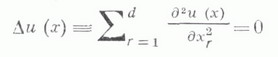
Краевые задачи для уравнения Лапласа являются частными случаями краевых задач для уравнения Пуассона и более общих уравнений эллиптического типа , а численные методы решения краевых задач для уравнений эллиптического типа содержат в себе многие численные методы для уравнения Лапласа. Специфика уравнения Лапласа позволяет конструировать и использовать методы, обладающие существенно лучшими характеристиками, чем методы для более общих уравнений, хотя на практике часто этим возможностям предпочитают простоту реализации метода на ЭВМ.

Основными численными методами для уравнений эллиптического типа являются: вариационно-разностные методы (проекционно-разностные, методы конечных элементов) и разностные методы (методы сеток). Оба класса методов связаны с аппроксимацией исходной области  некоторой сеточной областью  содержащей N узлов сетки, и построением системы алгебраических уравнений

относительно значений функции, определяемой в этих узлах. В вариационно-разностных методах, являющихся специальными случаями вариационных и проекционных методов, используется идея аппроксимации рассматриваемого пространства функций, содержащего решение исходной задачи, некоторыми специальными конечномерными подпространствами с заданными базисными функциями, а в системе (*) вектор  состоит из коэффициентов разложения получаемой аппроксимации искомого решения по выбранному базису. В предположении, что решение исходной задачи в ограниченной области W на плоскости имеет вид

где  - пространство Соболева, а функции  заданы и отражают асимптотическое поведение и (х) вблизи особых точек (угловых точек границы, точек перемены типа граничного условия), для многих типов областей  и смешанных краевых задач эти методы позволяют, например, найти решение u (х) с точностью e в  при затрате арифметических действий, а в ряде более частных случаев оценки вычислительной работы уменьшаются до

4.Решение задачи Дирихле в круге методом Фурье

Найти функцию U, удовлетворяющую уравнению:

 внутри круга

И граничному условию

 на границе круга,

Где - заданная функция, - полярный угол.

Введем полярную систему координат  с началом в центре круга.

- полярные координаты.

Уравнение (1) в полярных координатах имеет вид

Решим уравнение методом разделения переменных, то есть будем искать частное решение уравнения (1), вида

Подставляя предполагаемую форму решения в уравнение (3), получим

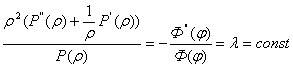
Отсюда получим два обыкновенных дифференциальных уравнения:

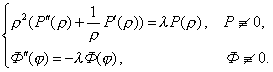
Определим знак :

1 случай. Пусть  например

Рассмотрим уравнение (5)

Характеристическое уравнение имеет вид

Это решение не подходит, так как при изменении угла  на величину  однозначная функция  должна вернуться к исходному значению  (условие периодичности).

Отсюда следует, что  является периодической функцией угла  с периодом .

2 случай Пусть , тогда

 - это решение подходит для уравнения (5) системы при условии, что А=0.

Рассмотрим уравнение (4) системы:

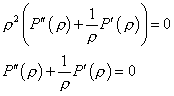
Пусть , тогда:

Таким образом, получаем: - решение уравнения в общем случае.

3 случай Пусть .

Решение уравнения (5):

 причем q.

Рассмотрим уравнение (4) системы:

Функцию  будем искать в виде

Подставим  в уравнение (4):

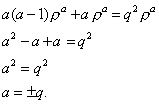
Следовательно, - решение уравнения, где C и D-постоянные. Для решения внутренней задачи надо положить , так как, если , то функция  обращается в бесконечность при и не является гармонической функцией внутри круга. Итак, частные решения нашей задачи найдены:

,

вид общего решения.

Удовлетворим краевому условию:

Считая , что задана как функция угла , возьмем ее разложение в ряд Фурье

Подставляя выражения для коэффициентов Фурье в формулу (6) и меняя порядок суммирования и интегрирования, получим

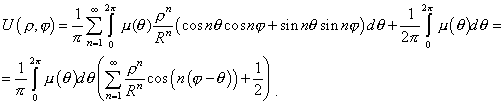
Произведем следующие тождественные преобразования:

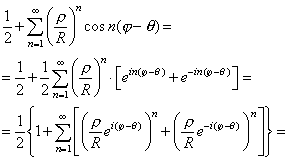
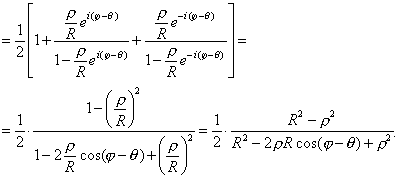
Подставляя полученный результат в равенство (8), получаем:

интегральная формула, дающая решение задачи.

Ядро Дирихле.

Заключение

Таким образом решения уравнения Лапласа очень гладкие они не имеют шишки максимумами или минимумами в R и, по сути "интерполировать" плавно между их значениями на границах Р. Докажем это важный факт, как применение теоремы о дивергенции.

Этот результат также следует, что если мы знаем, дивергенция вектора V и его ротора во всем мире, эти дифференцируемы всюду, и V обращается в нуль на бесконечности, то V определяется однозначно. Доказательство окна (если есть два решения V и V 'с тем же дивергенция и ротор, то на применении двойных поперечных личность продукт, который мы находим, что каждая компонента их разность подчиняется по уравнению Лапласа всюду. Его значение нигде, то его среднее значение по окружности на бесконечности, которая равна 0 по предположению. огромный же вывод справедлив, если V и V "должны вести себя на бесконечности таким же образом, так что V - V 'к 0 для больших аргументов.

Список использованной литературы

1.Эдвард Ч.Г., Пенни Д.Э. Дифференциальные уравнения и краевые задачи: моделирование и вычисление с помощью Mathematica, Maple и MATLAB. 3-е изд.-М.ООО "И.Д. Вильямс", 2008.-1104 с.

2. Гантмахер Ф.Р. математический анализ, 3-е изд.-М.: Наука, 1967.

3. Еругин Н.П. Линейные системы обыкновенных дифференциальных уравнений. - Минск, 1963.

4. Кручкович Г.И., Мордасов Г.М., Сулейманова Х.Р. и др. Сборник задач и упражнений по специальным главам высшей математики. Учебное пособие для втузов. М., "Высшая школа", 1970 г.