Курсовая работа: Транспортная задача по критериям стоимости и времени
Метод минимального элемента
Используют для нахождения начального опорного плана Т-задачи.
1. Элементы матрицы С нумеруют, начиная от минимального в порядке возрастания, а затем в этом же порядке заполняют матрицу Х0 :
Допустим, уже проделано k шагов метода, тогда среди незаполненной части матрицы X0 отыскиваем элемент с минимальным порядковым номером.
Пусть элементом с минимальным порядковым номером оказался
.
Возможны три случая:
а) если 
, то 
и всю оставшуюся i-ю строку заполняют нулями, а 
,
;
б) если 
, то 
и весь оставшийся j-й столбец заполняют нулями, а 
,
;
в) если 
, то 
и оставшийся j-й столбец и i-ю строку заполняют
нулями, а 
, 
.
На этом один шаг метода заканчивается.
Далее этот процесс повторяют с незаполненной частью матрицы X0.
Метод потенциалов:
Теорема. Если план 
транспортной
задачи является оптимальным , то ему соответствует система из 
чисел 
, удовлетворяющих условиям
для 
Числа 
называются потенциалами
соответственно 
го поставщика и 
го потребителя.
Для оптимального плана Т-задачи необходимо выполнение условий:
каждой занятой клетке в распределительной таблице соответствует сумма
потенциалов, равная тарифу этой клетки, т.е. 
;
каждой свободной клетке соответствует сумма потенциалов, не превышающая
тарифа этой клетки, т.е. 
.
Если хотя бы одна незанятая клетка не удовлетворяет второму условию, то опорный план является неоптимальным и его можно улучшить, переместив в данную клетку некоторое количество единиц груза
Данная теорема носит название теоремы о потенциалах. На ней основан специальный метод решения ТЗ, названный методом потенциалов.
Для применения метода потенциалов необходимо, чтобы заранее построенный
опорный план методом северо-западного угла (или другим методом) являлся
невырожденным, т.е. число базисных элементов равнялось 
. Если план является
вырожденным, то добавляют перевозку бесконечно малой величины ε. При этом
смотрят, чтобы план не перестал быть опорным.
Метод потенциалов позволяет, исходя из некоторого опорного плана перевозок, найти за конечное число итераций решение транспортной задачи.
Общая схема метода.
В начальном опорном плане каждому пункту ставят в соответствие некоторое
число, называемое его предварительным потенциалом. Предварительные потенциалы
выбирают так, чтобы их разность для любой пары пунктов Аi и Вj,
связанных основной коммуникацией, была равна сi,j. Если окажется,
что разность предварительных потенциалов для всех других коммуникаций не превосходит
, то данный план перевозок
- оптимальное решение задачи. В противном случае указывают способ улучшения
опорного плана Т-задачи.
Описание алгоритма метода потенциалов. Алгоритм складывается из предварительного этапа и конечного числа однотипных итераций.
Предварительный этап. С помощью известного метода определяют начальный
опорный план Х0 и вычисляют предварительные потенциалы 
.
Вычисление предварительных потенциалов производят так. По найденному плану Х0 строят схему Т-задачи из основных коммуникаций плана.
Поскольку на выполнение условий оптимальности плана оказывают влияние
лишь разности 
, то за начало
отсчета (нуль) можно принять потенциал любого из пунктов (как правило, за нуль
принимается 
).
После того как потенциалы всех пунктов найдены, строят матрицу
Если матрица C1 не содержит отрицательных элементов, то Х0 - оптимальный план. В противном случае Х0 - неоптимальный план, который может быть улучшен. Тогда переходят к выполнению однотипных итераций. Цель (k + 1)-й итерации - построение матрицы Сk, а также либо установление оптимальности плана Хk, либо нахождение более экономичного плана Хk+1.
Каждая итерация, кроме первой, где отсутствует первый этап, состоит из двух этапов.
Первый этап. Вычисляют матрицу Ck+1. Преобразование матрицы Ck в матрицу Ck+1 состоит в следующем. Выбирают наибольший по модулю отрицательней элемент матрицы Ck. Выделяют строку, в которой содержится этот элемент, а множество существенных элементов этой строки. При этом Xk-существенными элементами называют те элементы матрицы Ck, которые отвечают базисным перевозкам плана Xk.
Затем выделяют столбцы матрицы Ck, которые содержат элементы множества Xk-существенных элементов, которые находятся в столбцах матрицы Ck и отличны от элементов множества.
Процесс выделения продолжают до тех пор, пока очередное множество не окажется пустым. Поскольку каждые строка и столбец не могут быть выделены дважды, то весь процесс заканчивается за m+n-1 шагов.
Далее строят матрицу Ck+1. Для этого наибольший по модулю отрицательней элемент матрицы Ck прибавляют ко всем выделенным столбцам и вычитают из всех выделенных строк матрицы Ck. При этом все выделенные Xk-существенные элементы матрицы Ck остаются равными нулю.
Если все элементы матрицы Ck+1 окажутся неотрицательными, то Xk— оптимальный план, и на этом процесс заканчивается. В противном случае переходят ко второму этапу.
Второй этап. Производят улучшение плана Хk. Выбирают наибольший по модулю отрицательный элемент матрицы Ck+1. Затем составляют, применив, например метод вычеркивания, цепочку из положительных элементов плана Xk, которая замыкается на выбранном элементе.
После того как цепочка построена, в ней находят минимальный нечетный по порядку следования элемент и прибавляют его ко всем четным элементам цепочки и вычитают из всех нечетных элементов. Остальные элементы Xk оставляют без изменения.
Новый план Xk+1.построен. Он является опорным, так как число его ненулевых перевозок не изменилось.
4. Проверка достоверности полученных результатов
В общем случае проверка полученных результатов после очередной итерации вычисления осуществляется следующим образом:
Целевая функция считается 2 способами:
1.
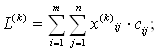
2. Пусть минимальным элементом матрицы С(k) оказался элемент с индексами μ, κ, тогда значение целевой функции на этом шаге будет равно:
Если значения не совпадают то, то на экран выводится ошибка.
Если условие выполняется, то полученный результат (на данной итерации) достоверен.
При выполнении дооптимизации единственным подтверждением правильности результатов может служить уменьшение целевой функции
.
5. Алгоритм решения задачи
1. Проверка правильности ввода данных.
2. Проверка условия баланса.
3. Построение начального опорного плана Х(0) методом минимального элемента.
4. Проверка плана на вырожденность, если нужно добавляем фиктивные перевозки.
5. Расчет начальных потенциалов и заполнение матрицы С(1).
6. Поиск минимального элемента в матрице С(1).
7. Если этот элемент меньше нуля, то заменяем нулевой элемент, соответствующий минимальному в С(1), в плане Х(0) на фиктивную перевозку, иначе на пункт 12.
8. Производим процедуру вычеркивания.
9. Оставшиеся не вычеркнутыми элементы разделяем на четные и нечетные, учитывая, что добавленный элемент принадлежит к четным.
10. Находим минимальный нечетный элемент и прибавляем его ко всем четным и отнимаем от нечетных элементов. Причем, если минимальных элементов окажется 2 или более, то один из них обнуляем, а остальные делаем фиктивными. В итоге получаем план Х(1).
11. Производим процедуру вычеркивания. Получаем матрицу С(2).
