Быстрый поиск

Курсовая работа: Применение метода ветвей и границ для задач календарного планирования

§4. Пример использования метода ветвей и границ

В качестве примера к методу ветвей и границ рассмотрим функцию z=4х1+х2+1®max (7) при ограничениях:

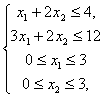(8). x1, x2 Î Z, (9).

Пусть Х0 = (0; 0), z0 = 1 - «оптимальное»[1] решение (10). Выполним 1-й этап общего алгоритма и найдем с помощью симплекс-метода, а затем и двойственного симплекс-метода (см. Приложение 1) X1, исходя из ограничений (8). Итак, X1 = (3; 0,5; 0; 1; 0; 2,5), z1 = 13,5 (11). Так как z1 дробное, то «оптимальным» так и остается план Х0,

Согласно 2-му пункту нашего плана, составим 2 новых системы ограничений для (7):

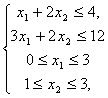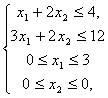(12) и (13).

Выполним 3-й пункт алгоритма. Для начала, решим задачу (7), (12) с помощью табличного процессора Microsoft Excel (см. Приложение 2) и получим X2 = (2; 1)[2], z2 = 10 (14). Так как z2 ≥ z0, «оптимальным» становится план Х0.

Решим задачу (7), (13). Из последнего уравнения очевидно, что x2 = 0. Отсюда следует, что x1 = 3 (максимально возможное). Тогда Х3 = (3; 0), z3 = 13 (15), а следовательно, данный план является оптимальным (теперь уже без кавычек).

Нам не пришлось выполнять 4-й пункт нашего алгоритма в связи с тем, что оптимальное решение найдено, переменные целочисленные. К тому же, все необходимые моменты решения уже были показаны в пунктах 1-3.

Пример, в котором всё складывается не так просто, приведен в Приложении 3.

календарное планирование программирование

III. Применение метода ветвей и границ для задач календарного планирования

Метод ветвей и границ является универсальным методом решения комбинаторных задач дискретного программирования. Сложность практического применения метода заключается в трудностях нахождения способа ветвления множества на подмножества и вычисления соответствующих оценок, которые зависят от специфики конкретной задачи.

Для того, чтобы выяснить области применения данного метода и ознакомиться с практической его формой, мы обратимся к задаче трех станков[3], как к классическому примеру.

§1. Алгоритм решения задачи трех станков методом ветвей и границ

Заданы n деталей di (i = 1, 2, ..., n), последовательно обрабатываемых на трех станках R1, R2, R3, причем технологические маршруты всех деталей одинаковы. Обозначим ai ,bi ,ci — длительность обработки деталей di на первом, втором и третьем станках соответственно.

Определить такую очередность запуска деталей в обработку, при которой минимизируется суммарное время завершения всех работ Tц.

Можно показать, что в задаче трех станков очередность выполнения первых, вторых и третьих операций в оптимальном решении может быть одинаковой (для четырех станков это свойство уже не выполняется). Поэтому достаточно определить очередность запуска только на одном станке (например, третьем).

Обозначим sk = (i1, i2 , ..., ik) — некоторую последовательность очередности запуска длиной k (1 £ k £ n) и A (sk), В (sk), С (sk) — время окончания обработки последовательности деталей sk на первом, втором и третьем станках соответственно.

Необходимо найти такую последовательность sопт, что

С(sопт) = min С (s). (16)

§1.1 Реккурентное вычисление A(sk), В(sk), C(sk) и условие доминирования

Покажем, как можно рекуррентно вычислять A (sk), В (sk), С (sk). Пусть sk+1 = (sk ,ik+i), т. е. последовательность деталей sk+1 получена из деталей sk с добавлением еще одной детали ik+1. Тогда:

A (sk+1) = A (sk)+ (17),

В (sk+1) = max [A (sk+1); В (sk)] + (18),

С (sk+1) = max [В (sk+1); С (sk)] + (19).

Логика выражений (17) – (19) очевидна, особенно если рассмотреть задачу двух станков.

Для задачи трех станков можно использовать следующее правило доминирования:

Если s — некоторая начальная последовательность, а — подпоследовательность, образованная из s перестановкой некоторых символов, то вариант s доминирует над , когда выполняются следующие неравенства:

А (s) £ А (), В (s) £ В (), С (s) £ С () (20),

причем хотя бы одно из них выполняется как строгое неравенство.

§1.2 Способ конструирования вариантов последовательностей s и вычисления оценок D(s) для каждого из них

Способ конструирования вариантов последовательностей s и вычисления оценок D(s) для каждого из них состоит в следующем:

Пусть имеется начальная подпоследовательность s. Тогда вычисляются величины:

dC(s) = С(s) +, (21)

dB(s) = В (s) + + , (22)

dA(s) = A (s) + + (23),

где J (s) — множество символов, образующих последовательность s.

За оценку критерия С(s) для варианта s можно принять величину

D(s) = max {dA(s), dB (s), dC (s)} (24).

Тогда ход решения задачи трех станков можно представить следующей формальной схемой:

1) Нулевой шаг. Задание множества G(0), образуется всеми возможными последовательностями (s = 0).

Вычисление оценки для множества G0:

D(0) = max {dA(0), dB (0), dC (0)} (25), где

; ; (26).

2) Первый шаг. Образование множеств G1(1), G2(1) , …, Gn(1), подмножество Gk определяется всеми последовательностями с началом ik(k, ...,n).

Вычисление оценок. Оценку для последовательности sk определяют из соотношения (24), т. е. D(sk) = max {dA(sk), dB (sk), dC (sk)}; k = 1,…,n. (27).

Выбор варианта для продолжения. Из всех подпоследовательностей, построенных на предыдущем шаге, выбирают наиболее перспективную последовательность sk с наименьшей оценкой, т. е. D(sk(1))=min D(sj(1)). (28)

Ветвление. Выбрав наиболее перспективный вариант последовательности sk(1), развивают его построением всех возможных подпоследовательностей длиной 2 с началом sk(1) вида sk+1(2)= (sk(1), j), где j не входит в sk.

Вычисление оценок производят в соответствии с соотношениями (21), (22), (23).

3) k-й шаг. Допустим, что уже проведено k шагов, в результате чего построены варианты s1(k), s2(k) ,…,sk(k), а именно подпоследовательности длиной k.

Выбираем самый перспективный вариант sS(k) такой, что

D(ss(k))=min D(sj(k)).

Множество Gs(k) разбиваем на (n — k) подмножеств, каждое из которых образуется добавлением к последовательности ss(k) некоторого элемента ik+1 такого, что ik+1.

Оценка определяется в соответствии с соотношениями (21) — (24).

В результате строим дерево вариантов следующего вида: вершина О отвечает s = 0, вершины первого уровня G1(1), G2(1)..., Gn(1) соответствуют последовательностям длиной 1, т. е. s1(1) = 1, s2(1) = 2,..., sn(1) = п и т. д. Каждая конечная вершина отвечает последовательности максимальной длины n.

Признак оптимальности. Если sv(n) отвечает конечной вершине дерева, причем оценка наименьшая из оценок всех вершин, то sv(n) — искомый вариант.