Курсовая работа: Практическое применение интерполирования гладких функций
Построить интерполяционный полином Лагранжа.
Решение. Из (8) следует:
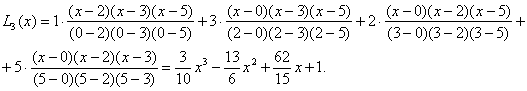
Задача 2.
Пользуясь интерполяционной формулой Лагранжа, составить уравнение прямой, проходящей через точки Р0(х0, у0) и Р1(х1, у1), если х0=-1, у0=-3, х1=2, у1=4.
Решение. В данном случае многочлен Лагранжа примет вид
.
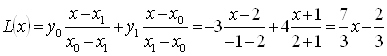Уравнение искомой прямой есть 
.
По строению 
(
). Но, в общем, это не так
и 
(
,
), так как интерполирование
предполагает приближенное нахождение:
(
)
И в связи с этим необходимо говорить о погрешности интерполирования. Заранее
сказав, 
разность этого выражения
нужно найти.
Замечание 1.
(
)
чем постоянно записывать равенство, слагаемое 
называют
остаточным членом (или погрешность интерполяции).
Теорема 1.
Если 
[a,b] [2]
(9) 
(
,
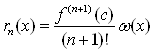), где 
[a,b] в промежутке беспрерывно n+1 раз
объясняет совокупность дифференцируемых функций.
[a,b] ó
[a,b];
Берем любую точку и зафиксируем ее (
,
), рассмотрим
вспомогательную функцию:
(10) 
, (
).
- свободный параметр,
который открыто объясняет 
(
).
Значение 
берем проходящим
через равенство 
. В это время
концы 
, будучи точками
промежутка, можно использовать теорему Ролля.
Существует 
: 
(
)
Сейчас для этой теоремы берем точки 
:
Существует 
: 
(
)
Когда закончим этот процесс, то получим следующее:
$
:
Итак, при t = x из (10) вытекает (9). Что и требовалось доказать.
Следствие 1:
Пусть 
.
В то время 
(
); над ними: 
.
Задача 3:
С помощью узлов
построить
полином 
для этой функции, при:
1) 
. Оценить погрешность
полинома;
2) в [a,b] найти максимальную погрешность полинома.
Решение: 
1) На основании Следствия 1 в непрерывном виде находим:
2) Использовав второе
равенство из Следствия 1 получаем:
.
Замечание 2:
Полученные с помощью этой формулы множества полиномов называются
полиномами Чебышева. В отдельных случаях: 
В теории приближения функции хорошо известен следующий факт: если в
качестве узлов интерполяции взять корни полинома 
,
то 
(
)
В этом случае из Следствия 1 следует, что
. Если свободная
интерполяция находится в отрезке [a,b],
то с помощью замены 
этот отрезок
можно заменить на [-1;1]. В это время точки
(11) 
(
, 
)
будут однородными с корнями 
, а
остаточный член записывается следующим образом:
.
Последнее неравенство полностью дает оптимальную оценку на отрезке [a,b], т.е. мы оцениваем погрешность интерполяции на отрезке [a,b], чтобы узлы (11) были оптимальными.
2. Один вид обобщенной интерполяции
Рассмотрим пример интерполяции для элементов множества 
. Для простоты и краткости
возьмем [a,b]=[-1;1], 
.
Пусть точки 
и 
будут разными между собой.
Поставим такую задачу:
(12) 
построить многочлен 
,
удовлетворяющий данным условиям. Здесь 
«собственный»
оператор класса 
:
Теорема 2.
Если взять в произвольной форме fÎC{m;0}, удовлетворяющее условию (12), то существует «обобщенный» интерполяционный полином и он единственен.
Доказательство:
Найдем интерполяционный полином в стандартном виде:
(13) 
Затем, учитывая (13) для того, чтобы найти коэффициенты 
(
), приходим к следующей
алгебраической системе:
(14) 
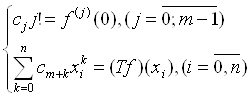
Эту систему упорядочим в матрицу S, являющуюся прямой суммой двух квадратных матриц размерностью m и n+1.
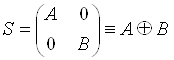
Здесь
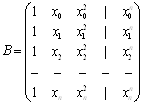
Значит, основываясь на фактах линейной алгебры, определяем
Что и требовалось доказать.
Сейчас поставим перед собой цель записать многочлен G(x) в явном виде. Будет полезно рассмотреть стандартный вид многочлена Лагранжа. Из (13) видно, что
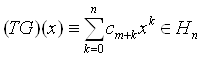
Поэтому имеет место следующее:
(14) 
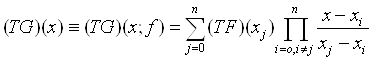
Возьмем параметры из (13):
(15) 
Таким образом, из (13), (14), (15) следует, что
(16) 
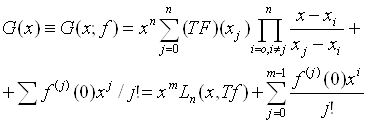
Замечание 3:
Если m=0, C{0;0}
C[-1;1],
(
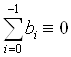). Значит, рассмотрев
функцию 
в задаче (11) приводится к
обычной интерполяционной задаче, а многочлен Лагранжа (16) превращается в
обычный интерполяционный многочлен. Таким образом, задача (11), действительно,
в значении одного определения становится обобщенной задачей интерполирования.
Сейчас поговорим о погрешности обобщенной интерполяции.
В этом случае 
нужно дать
оценку побольше. Выше приведены размышления и следствия, полученные в целях определения
одной системы функций.
.
Теорема 3.
Если
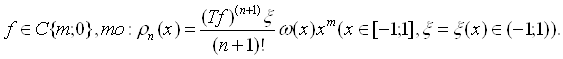
Здесь 
Доказательство:
Приняв во внимание (16) получаем
(17) 
Следующие приведения к формуле теоремы легко доказываются из (17) и теоремы 1.
Следствие 2.
Пусть 
В это время: 
2.2 Важное представление гладкой функции
Теорема 4.
Верна следующая связь:
(18) 
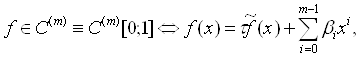
Вдобавок
(19) 
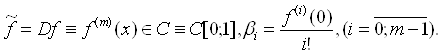
Доказательство: 
Пусть 
. По (19) получим 
в последовательной форме
используем метод интегрирования по частям, и изменяем его:
Отсюда выходит следующее неравенство:
(20) 
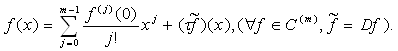
называют формулой Тейлора с
остаточным членом в интегральной форме.
Возьмем некоторую функцию 
, чтобы равенство (18) было
правильным 
. При рассмотрении второго
слагаемого полинома, достаточно показать что 
Î С(m).
При изучении производной 
полезно
использовать дифференцирование интеграла, зависящего от параметра. Эта формула
в математическом анализе очень известна и определяет следующее:
(21) 
здесь 
вдобавок 
Таким образом, находим в нашем случае необходимый вид:
Значит 
.
Замечание 6.
Рассмотрев, оператор 
из
последнего размышления вытекает полезное рассуждение:
(22) 
Заключение
Мы убедились, что в вычислительной математике существенную роль играет интерполяция функций, значения которой совпадают со значениями заданной функции в некотором числе точек.
В данной курсовой работе рассматривается интерполирование функции полиномами, непосредственно непрерывных функций на отрезке и в точке, определили понятие погрешности интерполяции.
У нас возникла задача о восстановлении непрерывной функции по ее табличным значениям, поэтому в данной работе были приведены конкретные примеры по построению интерполяционного полинома Лагранжа, по оцениванию погрешности интерполяционного полинома.
В нашем случае для более полного раскрытия данной темы подробно проиллюстрировано само понятие интерполяции, далее интерполирование непосредственно гладкой функции и интерполирование гладкой функции в точке.
Список использованной литературы
1. Н.С.Габбасов. Некоторые применения производной. Наб.Челны, 1998г.
2. Я.С.Бугров, С.М.Никольский. Дифференциальное и интегральное исчисление. М.: «Наука», 1984г.
3. С.М.Никольский. Курс математического анализа. М.: «Наука», 1990г.
4. Л.Д.Кудрявцев. Краткий курс математического анализа. М.: «Наука», 1989г.
5. И.А.Марон. Дифференциальное и интегральное исчисление. М.: «Наука», 1970г.
6. А.А.Самарский. Введение в численные методы. М.: «Наука», 1987.
[1] Здесь Hn – это множество всех алгебраических многочленов степени n.
[2] На непрерывном отрезке и в точке обозначили множество функции, имеющей производную по Тейлору m-го порядка.
(естественно,
Верно следующее соответствие:
здесь
