Курсовая работа: Анализ, оценка и обеспечение надежности миниатюрного микромощного радиопередатчика

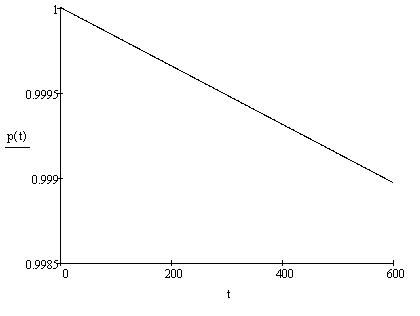
Рисунок 5.1 – График зависимости вероятности безотказной работы от времени при внезапных отказах исследуемого ФУ

5.3 Уточненный расчет надежности по деградационным отказам

Аналогично подразделу 5.1 для биполярного высокочастотного малошумящего транзистора были определены базовая интенсивность отказов λ0=0,18∙10 ч и по (5.6)-(5.9) некоторые коэффициенты влияния (см. табл. 5.4).

, (5.6)

где  – температура перехода, °С по (5.7).

,(5.7)

где =50 °С – температура окружающей среды;

=70 °С/Вт – тепловое сопротивление «переход-корпус»;

P – мощность рассеивания, P=3,2 мВт.

Результат = 50,224 °С.

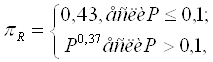(5.8)

где P – номинальная мощность, P=0.25 Вт.

(5.9)

где  – коэффициент электрической нагрузки, 0<S<1.0;

 – соответственно, рабочее напряжение коллектор-эмиттер =2,2 В и предельное напряжение коллектор-эмиттер при оторванной базе=2.6 В.

Таблица 5.4 – Значение коэффициентов влияния, констант и уточненное значение интенсивностей отказов для транзистора

ЭРИ	λ0∙10 ч				λут.тр.∙106 ч
VT1	0.18	1.7395	0.6	0.118	0.222

По номограмме была определена средняя наработка до отказа для транзистора VT1 (To=3,7∙105 ч).

Уточненное значение средней наработки до отказа всех элементов, подверженных деградации было рассчитано по (5.10).

,(5.10)

TYT=μ=3,7 – параметр масштаба деградационного немонотонного распределения.

По (5.11) была найдена вероятность деградационных отказов:

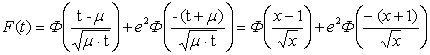, (5.11)

где  - функция Лапласа;

Соответственно вероятность безотказной работы для совокупности элементов подверженных деградации определяется по (5.12).

(5.12)

График зависимости вероятности безотказной работы от времени исследуемого ФУ по деградационным отказам представлен на рис. 5.2.

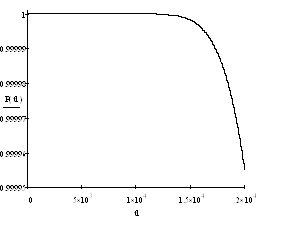
Рисунок 5.2 – График зависимости вероятности безотказной работы от времени при деградационных отказах исследуемого ФУ

Уточненная вероятность безотказной работы исследуемого ФУ была рассчитана по формуле (5.13).

Рут.(t)=Рут.I(t)·Рут.II(t).(5.13)

Рут.(tб.р.)=0.999

График зависимости уточненной вероятности безотказной работы от времени ФУ №2 представлен на рис. 5.3.

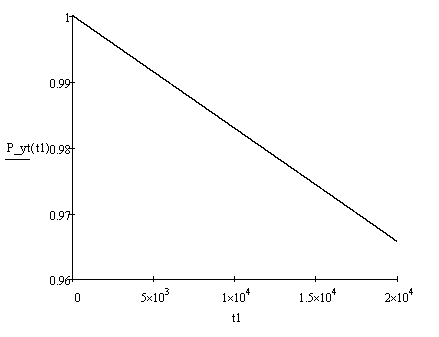
Рисунок 5.3 – График зависимости уточненной вероятности безотказной работы от времени ФУ №2

6. РАСЧЕТ ПОЛЯ ДОПУСКА НА ОПРЕДЕЛЯЮЩИЙ ПАРАМЕТР ФУ №2

Для ФУ №2 была выделена та часть, которая является определяющей с точки зрения работоспособности. Эта часть выделена пунктиром на схеме ЭП (см. прил. А). Определяющими элементами в выделенной части являются транзистор VT1, резисторы R3 и R4, определяющим параметром является коэффициент усиления:

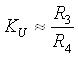. (6.1)

Было предположено, что ,  и соответственно получена зависимость:

y=f(x1,x2),(6.2)

где y=46.8– выходной параметр.

По (6.3) были рассчитаны коэффициенты влияния Квi.

Квi=,(6.3)

где xi0, y0 – номинальные значения входных и выходного параметров.

Квx1=1,93∙10-5, Квx2=8,23∙10-4.

По данным комплектующих элементов были определены средние значения поля допуска на относительную погрешность каждого первичного параметра:

М,(6.4)

где  - допустимые максимальные и минимальные значения поля допуска.

Однако для всех элементов заданного ФУ допуск на их параметры является симметричным, а значит при подстановке этих значений в формулу (6.4), эта величина будет равна нулю, т.е. М = =0.

По (6.5) было определено среднее значение поля допуска на определяющий параметр.

М.(6.5)

М=0.

В предположении нормального закона распределения выходного параметра и независимости первичных параметров была рассчитана половина поля допуска на относительную погрешность выходного параметра:

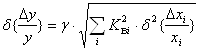,(6.6)

где  – половина поля допуска на относительную погрешность i-го первичного параметра;

γ – коэффициент гарантированной надежности, гарантирует некоторую вероятность нахождения параметров в поле допуска.

В данном случае для заданной вероятности безотказной работы объекта, равной 0.96, справочное значение γ=0.668. =12.

По (6.7), (6.8) были рассчитаны предельные значения, верхнее и нижнее (δв, δн), на относительную погрешность определяющего параметра.

,(6.7)

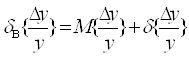.(6.8)

δв=12 , δн=-12.

По (6.9), (6.10) были рассчитаны нижнее и верхнее предельные значения определяющего параметра.

ymin=y0-||∙y0/100%,(6.9)

ymax=y0+||∙y0/100%,(6.10)

ymin=41,2, ymax=52,4.

Таким образом, допуск на определяемый параметр (в данном случае коэффициент усиления KU) следующий:

.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8