Курсовая работа: Анализ на чувствительность двойственных оценок

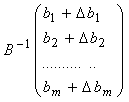
Таким образом, если найдено решение задачи (7.7)–(7.9), то нетрудно провести анализ устойчивости двойственных оценок относительно изменений . Это, в свою очередь, позволяет:

1. проанализировать устойчивость оптимального плана задачи (7.10), (7.11) относительно изменений свободных членов системы линейных уравнений (7.8),

2. оценить степень влияния изменения , на максимальное значение целевой функции задачи (7.7)–(7.9), что дает возможность определить наиболее целесообразный вариант возможных изменений .

Вывод

В теоретической части пояснительной записки к курсовой работе приведен краткий теоретический материал о формах представления задач линейного программирование, симплексный метод и метод двойственной задачи, необходимый для решения задач линейного программирования.

линейный симплекс программирование двойственный

2. Практическая часть

2.1 Постановка задачи

Для изготовления трех видов продукции грузовик, легковой автомобиль и мотоцикл игрушечная фабрика использует три вида продукции, их наличие в распоряжении предприятия, а так же цена единицы продукции приведены в таблице 2

Таблица 2

Исходные данные

№	Вид сырья	Нормы затрат сырья			Наличие ресурса
		A	B	C
1	грузовик	1	1	1	430
2	Легковой автомобиль	3	0	2	460
3	мотоцикл	1	4	0	420
4	Цена ед. продукции	3	2	5

Требуется:

сформулировать двойственную задачу и найти оптимальные планы прямой и двойственной задачи.

найти интервалы устойчивости двойственных оценок по отношению к изменениям ресурсов каждого типа.

выявить изменения общей стоимости изготовляемой продукции, определяемой оптимальным планом ее производства при уменьшении количества ресурса I типа на 130 единиц и увеличения количества ресурсов II и III типа на 120 и 110 единиц.

Провести анализ возможного изменения общей стоимости продукции как при изменении объемов каждого из ресурсов по отдельности, так и при одновременном изменении в указанных размерах.

2.2 Математическая модель исходной задачи

Пусть xj – количество изделий j –го вида; aij – затраты времени на единицу продукции вида j на оборудовании i-го типа, cj – стоимость единицы изделия вида j, si – общий фонд рабочего времени на оборудовании типа i.

Целевая функция:

L = 3x1 + 2x2 + 5x3 → max

Ограничения:

x1 +x2 +x3 + x4=430

3x1 + 2x3 + x5 = 46

x1 + 4x2 +x6 =420

xj ≥ 0 , j = 1,6

Составляется матрица из коэффициентов при неизвестных в системе ограничений исходной задачи.

А=

2.3 Математическая модель двойственной задачи

Число переменных в двойственной задаче равно числу уравнений в системе исходной задачи, т. е. равно семи.

Целевая функция исходной задачи исследуется на максимум, а система условий содержит только уравнения. Поэтому в двойственной задаче целевая функция исследуется на минимум, а ее переменные могут принимать любые значения (в том числе и отрицательные). Следовательно, для исходной задачи двойственная задача такова:

Найти минимум функции:

Ограничения:

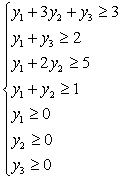
И составляется аналогичная матрица, которая получается транспонированием (т.е. заменой строк столбцами, а столбцов – строками).

АТ=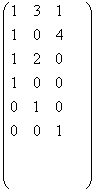

2.4 Нахождение решения исходной задачи

Задача записывается в форме основной задачи линейного программирования.

Целевая функция:

L = 3x1 + 2x2 + 5x3 → max

Ограничения:

x1 +x2 +x3 + x4=430

3x1 + 2x3 + x5 = 46

x1 + 4x2 +x6 =420

xj ≥ 0 , j = 1,6

Сначала проверяется, можно ли решить задачу симплексным методом:

m < n; bi ≥ 0, i= 1,3; задача записана в форме основной задачи линейного программирования. Имеется исходный опорный план X =(0,0,0,0,430,460,420). Далее заполняется первая симплексная таблица (таблица 3):

Таблица 3

Симплекс-таблица (1-ая итерация)

Страницы: 1, 2, 3, 4, 5, 6, 7, 8