 Курсовая работа: Алгоритмы преобразования ключей
Курсовая работа: Алгоритмы преобразования ключей
Наиболее часто встречается операция поиска записи по идентифицирующему его полю - ключу. Поэтому файл, как правило, индексируется по ключевому полю. Поиск по ключу в общем виде может рассматриваться как преобразование значения ключевого поля в адрес записи в файле (или номер записи), то есть как функция вида f(key) -> m.
Очевидно, можно сформулировать обратную задачу: если некоторым образом подобрать функцию f(), то ее можно использовать для определения места в файле, куда следует поместить запись с ключом key. Основное требование к такой функции: она должна как можно более равномерно распределять записи с различными значениями ключа по файлу, то есть иметь "случайный" вид. Кроме того, необходимо каким-то образом решить проблему "коллизий", то есть попадания нескольких записей с различными ключами в один физический адрес (номер записи).
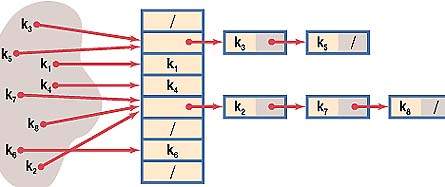
Функция f() называется распределяющей или рассеивающей функцией. Пример одной из таких функций: берется квадрат значения ключа, из него извлекаются n значащих цифр из середины, которые и дают значение номера записи в файле:
int Place1024(key) // Функция рассеивания для файла из
unsigned key; // 1024 записей и 16 разрядного
{ // ключа
unsigned long n,n1;
int m;
n = (unsigned long)key * key;
for (m=0, n1 = n; n1 !=0; m++, n1 >>= 1); // Подсчет количества значащих
if (m < 10) return(n); // битов в n
m = (m - 10) / 2; // m - количество битов по краям
return( (n >> m) & 0x3FF);
}
Известны два способа решения проблемы коллизий. В первом случае файл содержит область переполнения. Если функция f() вычисляет адрес записи в файле, а соответствующее место уже заполнено записью с другим значением ключа, то новая запись помещается в область переполнения. При этом возможны два варианта:
- записи в области переполнения не связаны между собой, и для поиска в ней используется последовательный просмотр всех записей;
- в области переполнения организуются списки записей, участвующих в коллизии: то есть запись в основной области является заголовком списка записей в области переполнения, куда попадают все записи, вступающие в коллизию.
В другом случае запись, вступившая в коллизию, помещается в некоторое свободное место файла, начиная от текущей занятой позиции. Возможные варианты поиска:
- первая свободная позиция, начиная от текущей;
- проверяются позиции, пропорциональные квадрату шага относительно текущей занятой, то есть m = ( f(key) + i * i ) mod n, где i - номер шага, n - размер таблицы. Такое размещение позволяет лучше "рассеивать" записи при коллизии.
Рассматриваемый метод обозначается терминами расстановка или хеширование (от hash - смешивать, перемалывать).
Одним из существенных недостатков метода является необходимость заранее резервировать файл для размещения записей с номерами от 0 до m - в диапазоне возможных значений функции рассеивания. Кроме того, при заполнении файла увеличивается количество коллизий и эффективность метода падает. Если же количество записей возрастает настолько, что файл необходимо расширять, то это связано с изменением функции рассеивания и перераспределением (перезаписью) уже имеющихся записей в соответствии с новой функцией.
ГЛАВА 2. ПРАКТИЧЕСКАЯ ЧАСТЬ
2.1. Вставка элемента в в-дерево
Рассмотрим структуру узла B-дерева.
В каждом узле мы будем хранить не более NumberOfItems записей. Также нам надо будет хранить текущее количество записей в узле. Для удобства возврата назад к корню дерева будем запоминать для каждого узла указатель на его узел-предок.
Type
PBTreeNode = ^TBTreeNode;
TBTreeNode = record {узел дерева}
Count: Integer;
PreviousNode: PBTreeNode;
Items: array[0..NumberOfItems+1] of record
Value: ItemType;
NextNode: PBTreeNode;
end;
end;
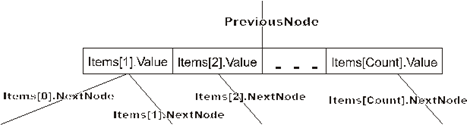
У элемента Items[0] будет использоваться только поле NextNode. Дополнительный элемент Items[NumberOfItems+1] предназначен для обработки переполнения, о чем будет рассказано ниже, где будет обсуждаться алгоритм добавления элемента в B-дерево.
Поскольку дерево упорядочено, то Items[1].Value<Items[2].Value<…< Items[Count].Value. Указатель Items[i].NextNode указывает на поддерево элементов, больших Items[i].Value и меньших Items[i+1].Value. Понятно, что указатель Items[0].NextNode будет указывать на поддерево элементов, меньших Items[1].Value, а указатель Items[Count].NextNode – на поддерево элементов, больших Items[Count].Value.
Само дерево можно задать просто указанием корневой вершины. Естественно, что у такой вершины PreviousNode будет равен nil.
Type
TBTree = TBTreeNode;
Прежде чем рассматривать алгоритмы, соберем воедино все требования к B-дереву:
1. каждый узел имеет не более NumberOfItems сыновей;
2. каждый узел, кроме корня, имеет не менее NumberOfItems/2 сыновей;
3. корень, если он не лист, имеет не менее 2-х сыновей;
4. все листья расположены на одном уровне (дерево сбалансировано);
5. нелистовой узел с k сыновьями содержит не менее k-1 ключ.
Из всего вышесказанного можно сразу сформулировать алгоритм поиска элемента в B-дереве.
Поиск элемента в B-дереве
Поиск будем начинать с корневого узла. Если искомый элемент присутствует в загруженной странице поиска, то завершаем поиск с положительным ответом, иначе загружаем следующую страницу поиска, и так до тех пор, когда либо найдем искомый элемент, либо не окажется «следующей страницы поиска» (пришли в лист B-дерева).
Посмотрим на примере, как это будет работать. Пусть мы имеем такое дерево (в наших примерах мы будем разбирать небольшие деревья, хотя в реальности B-деревья применяются при работе с большими массивами информации):
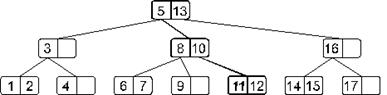
Будем искать элемент 11. Сначала загрузим корневой узел. Эта страница поиска содержит элементы 5 и 13. Наш искомый элемент больше 5, но меньше 13. Значит, идем по ссылке, идущей от элемента 5. Загружаем следующую страницу поиска (с элементами 8 и 10). Эта страница тоже не содержит искомого элемента. Замечаем, что 11 больше 10 – следовательно, двигаемся по ссылке, идущей от элемента 10. Загружаем соответствующую страницу поиска (с элементами 11 и 12), в которой и находим искомый элемент. Итак, в этом примере, чтобы найти элемент, нам понадобилось три раза обратиться к внешней памяти для чтения очередной страницы.
Если бы в нашем примере мы искали, допустим, элемент 18, то, просмотрев 3 страницы поиска (последней была бы страница с элементом 17), мы бы обнаружили, что от элемента 17 нет ссылки на поддерево с элементами большими 17, и пришли бы к выводу, что элемента 18 в дереве нет.
Теперь точно сформулируем алгоритм поиска элемента Item в B-дереве, предположив, что дерево хранится в переменной BTree, а функция LookFor возвращает номер первого большего или равного элемента узла (фактически производит поиск в узле).
function BTree.Exist(Item: ItemType): Boolean;
Var
CurrentNode: PBTreeNode;
Position: Integer;
begin
Exist := False;
CurrentNode := @BTree;
Repeat
Position := LookFor(CurrentNode, Item);
if (CurrentNode.Count>=Position)and
(CurrentNode.Items[Position].Value=Item) then
begin
Exist := True;
Exit;
end;
if CurrentNode.Items[Position-1].NextNode=nil then
Break
else
CurrentNode := CurrentNode.Items[Position-1].NextNode;
until False;
end;
Здесь мы пользуемся тем, что, если ключ лежит между Items[i].Value и Items[i+1].Value, то во внутреннюю память надо подкачать страницу поиска, на которую указывает Items[i].NextNode.
Заметим, что для ускорения поиска ключа внутри страницы поиска (функция LookFor), можно воспользоваться дихотомическим поиском, который описан ранее в главе, где разбирались способы хранения множества элементов в последовательном массиве.
Учитывая то, что время обработки страницы поиска есть величина постоянная, пропорциональная размеру страницы, сложность алгоритма поиска в B-дереве будет T(h), где h – глубина дерева.
Добавление элемента в B-дерево
Для того чтобы наше дерево можно было считать эффективной структурой данных для хранения множества значений, необходимо, чтобы каждый узел заполнился хотя бы наполовину. Дерево строится снизу. Это означает, что любой новый элемент добавляется в листовой узел. Если при этом произойдет переполнение (на этот случай в каждом узле зарезервирован лишний элемент), то есть число элементов в узле превысит NumberOfItems, то надо будет разделить узел на два узла, и вынести средний элемент на верхний уровень. Может случиться, что при этой операции на верхнем уровне тоже получится переполнение, что вызовет еще одно деление. В худшем случае эта волна докатится до корня дерева.
В общем виде алгоритм добавления элемента Item в B-дерево можно описать следующей последовательностью действий:
1. Поиск листового узла Node, в который следует произвести добавление элемента Item.
2. Добавление элемента Item в узел Node.
3. Если Node содержит больше, чем NumberOfItems элементов (произошло переполнение), то
o делим Node на две части, не включая в них средний элемент;
o Item=средний элемент Node;


