 Контрольная работа: Задача о составлении маршрута коммивояжера. Метод ветвей и границ
Контрольная работа: Задача о составлении маршрута коммивояжера. Метод ветвей и границ
Таким образом, следует по возможности сократить путь, проходимый роботом.
Итак, задачу уменьшения денежных затрат мы свели к задаче поиска пути минимальной длинны. Имеем задачу коммивояжера.
5.2 Выявление основных особенностей рассматриваемого объекта
Будем
считать, что у нас имеются собранные статистические данные, показывающие время
движения робота между агрегатами цеха (См. табл. 1). Здесь ![]() – номера агрегатов.
– номера агрегатов. ![]() – соответствует времени
движения выраженном в некоторых условных единицах. Таблица симметрична.
Незаполненные поля говорят о невозможности данного маршрута по каким-то
причинам.
– соответствует времени
движения выраженном в некоторых условных единицах. Таблица симметрична.
Незаполненные поля говорят о невозможности данного маршрута по каким-то
причинам.
Таблица 1.
|
|
1 | 2 | 3 | 4 | 5 |
| 1 | * | 4 | 2 | 5 | |
| 2 | * | 1 | 9 | ||
| 3 | * | 3 | 4 | ||
| 4 | * | 11 | |||
| 5 | * |
5.3 Пример решения задачи коммивояжера
Имеем «чисто» математическую задачу, которую решим, используя метод Ветвей и Границ.
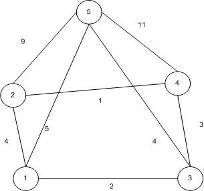
В симметричном графе, изображенном на рис. 3, определить кратчайший путь из вершины 1 в вершину 2, проходящим через все вершины графа только по одному разу.
Шаг 0.
Значение![]() . Пометим вершину 1
признаком
. Пометим вершину 1
признаком ![]()
Шаг 1.
Пометим вершину 3 признаками ![]()
Рис. 3. Шаг
З. Имеем ![]() .
.
Шаг
1. Пометим следующие вершины: вершину 4 – признаками ![]() вершину 5 – признаками
вершину 5 – признаками ![]()
Шаг 3. Имеем ![]() .
.
Шаг 1.
Пометим вершину 5 признаками ![]()
Шаг 3. Имеем ![]() .
.
Шаг 1.
Пометим вершину 3 признаками ![]()
Шаг 3. Имеем ![]() .
.
Шаг 1.
Пометим вершину 4 признаками ![]()
Шаг 1.
Пометим вершину 2 – признаками ![]() так
как
так
как ![]() , то искомый путь построен.
, то искомый путь построен.
Шаг 2. Искомый путь составляет последовательность вершин 1, 5, 3, 4, 2.
Общее затрачиваемое время в пути составит 13.
Выводы
В данной работе мы познакомили читателя с основными понятиями теории графов, дали представление о задаче коммивояжера, описали метод ветвей и границ. Также привели пример использования метода ветвей и границ для решения задачи коммивояжера.
Еще раз отметим, что задача коммивояжера является одной из самых важнейших задач в теории графов. Возможность представления (записи) различных производственных процессов на языке теории графов и умение решить сформулированную математическую задачу позволяют найти оптимальную стратегию ведения хозяйства, сэкономить ресурсы, выполнить поставленную задачу в более короткие сроки. Очевидно, что изучение методов теории графов, методов математического программирования, системного анализа и пр. – является важным этапом подготовки инженеров в МГСУ.
Список литературы
1. Н.М. Новикова «Основы оптимизации», курс лекций. М. 1998.
2. Н. Кристофидес «Теория графов. Алгоритмический подход», М., Мир, 1978.
3. С.Е. Канторер. «Методы обоснования эффективности применения машин в строительстве». М. 1969.
4. Институт математики им. С.Л. Соболева СО РАН Лаборатория «Математические модели принятия решений», статья «Метод ветвей и границ». Адрес в интернете: http://math.nsc.ru/AP/benchmarks/index.html.
5. Е.А. Тишкин «Эвристический алгоритм решения задачи коммивояжера». Публикация на сайте http://nit.itsoft.ru. Самарский государственный аэрокосмический университет, Россия.


