Контрольная работа: Моделирование процесса печати с использованием струйного принтера Hewlett Packard (термоструйная печать)
Граф композиции:
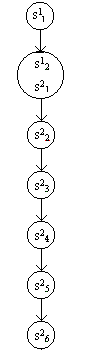
Вывод: композиция необходима для объединения нескольких процессов в
один. В данном случае использовалась последовательная композиция, чтобы
смоделировать процесс печати в целом, состоящий из полготовки к печати и
непосредственно самой печати. Получившийся процесс 
представляет собой несколько
упрощенный исходный процесс.
Предметная интерпретация асинхронного процесса.
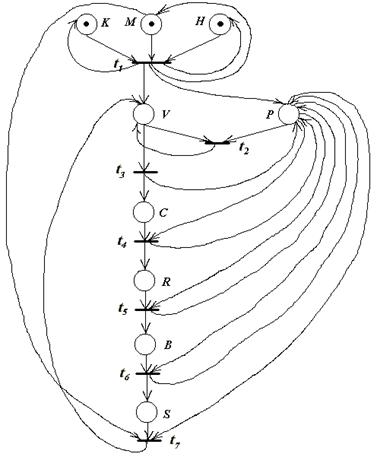
Построение сети Петри.
Сеть Петри для данного процесса – пятерка N = <P, T, H, F, M0>, где
P = {K, M, P, V, C, R, S, H, B} – множество условий;
T = {t1, t2, t3, t4, t5, t6, t7} – множество событий;
M0 = (1,1,0,0,0,0,0,1,0) – начальная разметка;
F и H – функции инцидентности, описывающие наличие дуги
| K | M | P | V | C | R | S | H | B | |
|
s1 = |
1 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 |
|
s2 = |
1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 0 |
|
s3 = |
1 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
|
s4 = |
1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 0 |
|
s5 = |
1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | 0 |
|
s6 = |
1 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 |
|
s7 = |
1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 |
|
s8 = |
1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
|
F(K, t1) = 1 |
H(t1, K) = 1 |
|
F(M, t1) = 1 |
H(t1, M) = 1 |
|
F(H, t1) = 1 |
H(t1, H) = 1 |
|
F(P, t2) = 1 |
H(t1, P) = 1 |
|
F(V, t2) = 1 |
H(t1, V) = 1 |
|
F(V, t3) = 1 |
H(t2, V) = 1 |
|
F(P, t4) = 1 |
H(t3, P) = 1 |
|
F(C, t4) = 1 |
H(t3, C) = 1 |
|
F(P, t5) = 1 |
H(t4, P) = 1 |
|
F(R, t5) = 1 |
H(t4, R) = 1 |
|
F(P, t6) = 1 |
H(t5, P) = 1 |
|
F(B, t6) = 1 |
H(t5, B) = 1 |
|
F(P, t7) = 1 |
H(t6, P) = 1 |
|
F(S, t7) = 1 |
H(t6, S) = 1 |
|
F(M, t7) = 1 |
H(t7, V) = 1 |
Граф разметок сети
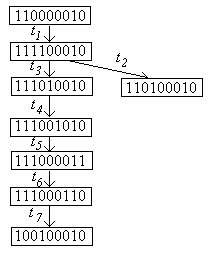
Покрывающее дерево выглядит аналогичным образом.
Свойства построенной сети Петри
Ограниченность и безопасность:
ü сеть ограничена, так как все ее условия ограничены (ни одна вершина покрывающего дерева не содержит символа ω);
ü сеть является безопасной, т.к. все ее условия безопасны (любая достижимая в сети разметка представляет собой вектор из 0 и 1).
Живость и устойчивость:
ü сеть не является живой, т.к. все её переходы живы при 
, но не являются живыми при любой
другой достижимой в сети разметке;
ü сеть не является устойчивой, т.к. переход t2 не является устойчивым.
Вывод: построенная сеть Петри дает представление о функционировании компонент процесса. Она является ограниченной и безопасной, но не является устойчивой и живой.
Заключение
В данном РГЗ была построена модель «асинхронный процесс» печати струйного принтера. Полученный асинхронный процесс является эффективным, неуправляемым и непростым.
Над процессом были произведены операции: редукции, репозиции и параллельной композиции.
Репозиция исходного процесса показывает, что нет необходимости использовать дополнительные ситуации для повторного возобновления процесса работы принтера в ситуациях:
ü возобновление печати на новом листе;
ü циклическое повторение нагрева чернил, образования пузыря и выброс капли на бумагу;
ü возобновление печати после вывода сообщения об отсутствии бумаги.
Репозиция является частичной.
Редукция позволяет существенно упростить рассматриваемый процесс, сведя его к механизму печати струйного принтера (перемещение каретки, нагрев чернил, образование пузыря, выброс капли на бумагу и наполнение камеры чернилами).
Композиция необходима для объединения нескольких процессов в один, для дальнейшего рассмотрения поведения этих процессов в системе. В данном случае использовалась параллельная композиция.
Для данного процесса была построена сеть Петри. Она является ограниченной и безопасной, но не является устойчивой и живой.
модель печать струйный принтер
Литература
1. Лазарева И.М. Конспект лекции по теории вычислительных процессов.
