 Контрольная работа: Моделі та структури даних
Контрольная работа: Моделі та структури даних
SUCCESSOR (x)
1 if right [x] <> NULL
2 then return MINIMUM (right [x])
3 y: =p [x]
4 while y<>NULL and x = right [y]
5 do x: =y
6 y: =p [y]
7 return y
Процедура знаходження попереднього даному елемента є симетричною. Обидві процедури знову ж таки знаходять елемент за час, пропорційний O (h)
Додавання елементу.
Процедура додавання елементу в бінарне дерево T додає елемент, зберігаючи умову впорядкованості.
Параметром тут є вказівник z на нову вершину, в яку поміщене значення val [z], left [z] =right [z] =NULL.
INSERT (T, z)
1 y: =NIL
2 x: =root [T]
3 while x <> NULL
4 do y: =x
5 if val [z] < val [x]
6 then x: =left [x]
7 else x: =right [x]
8 p [z]: =NULL
9 if y = NULL
10 then root [T]: =z
11 else if val [z] <val [y]
12 then left [y]: =z
13 else right [y]: =z
Процедура рухається вниз по дереву, при цьому зберігаючи в y вказівник на батька вершини x. Порівнюючи значення в x та z, процедура вирішує, в яке з піддерев рухатись далі. Процес завершується тоді, коли x=NULL. Саме сюди й слід помістити вершину z (рядки 8-13). Ця операція також потребує часу для виконання, пропорційного O (h). Видалення елементу Параметром для процедури є вказівник на вершину, що видаляється. Тут можливі три варіанти дій: якщо у вершини немає дітей, достатньо помістити NULL у відповідне поле його батька (замість вказівника на вершину, що видаляється) якщо у вершини є одна дитина, можна з'єднати батька цієї вершини безпосередньо з її дитиною якщо вершина має двох дітей, слід спочатку знайти слідуючий (в сенсі порядку) елемент y, в якого немає лівої дитини, а потім скопіювати значення та додаткові дані з вершини y на місце вершини, що видаляється, а саму вершину y видалити.
DELETE (T, z)
1 if left [z] = NULL or right [z] =NULL
2 then y: =z
3 else y: =SUCCESSOR (z)
4 if left [y] <> NULL
5 then x: =left [y]
6 else x: = right [y]
7 if x <> NULL
8 then p [x]: =p [y]
9 if p [y]: =NULL
10 then root [T]: =x
11 else if y=left [p [y]]
12 then left [p [y]]: =x
13 else right [p [y]]: =x
14 if y <> z
15 then val [z]: =val [y]
16 // копіювання додаткових даних з y
17 return y
Відкриття програми
2. Списки
Внести до її тексту зміни та виконати її, створивши список, розмір якого визначено відповідно до варіанту № 15.
Список (list) - набір елементів, розташованих у певному порядку. Таким набором бути може ряд знаків у слові, слів у пропозицій у книзі. Цей термін може також ставитися до набору елементів на диску. Використання при обробці інформації списків як типи даних привело до появи в мовах програмування засобів обробки списків. Список черговості (pushup list) - список, у якому останній вступник елемент додається до нижньої частини списку. Список з використанням покажчиків (linked list) - список, у якому кожний елемент містить покажчик на наступний елемент списку. Лінійний список (linear list) - це безліч, що складається з вузлів, структурні властивості якого по суті обмежуються лише лінійним (одномірним) відносним положенням вузлів, тобто тими умовами, що якщо, те є першим вузлом; якщо, те k-му вузлу передує й за ним треба; є останнім вузлом. Операції, які ми можемо право виконувати над лінійними списками, є наступними:
1. Одержати доступ до k-го вузла списку, щоб проаналізувати й/або змінити вміст його полів.
2. Включити новий вузол безпосередньо перед k-им вузлом.
3. Виключити k-й вузол.
4. Об'єднати два (або більше) лінійних списки в один список.
5. Розбити лінійний список на два (або більше) списки.
6. Зробити копію лінійного списку.
7. Визначити кількість вузлів у списку.
8. Виконати сортування вузлів списку в зростаючому порядку по деяких інформаційних полях у вузлах.
9. Знайти в списку вузол із заданим значенням у деякім полі.
бінарне дерево структура масив
Спеціальні випадки k=1 і k=n в операціях (1), (2) і (3) особливо виділяються, оскільки в лінійному списку простіше одержати доступ до першого й останнього елементів, ніж до довільного елемента.
Проводимо компілюцію
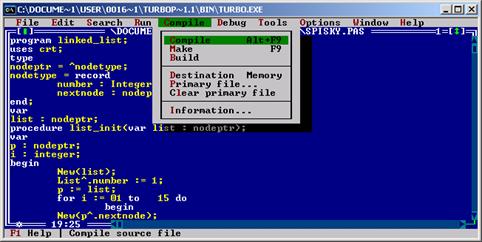
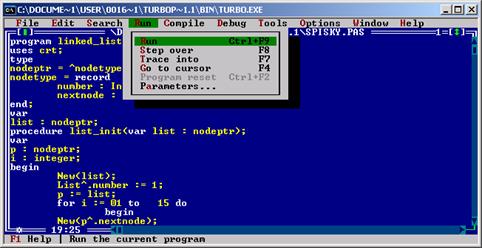
3. Вводимо дані стеку
Виконати її, ввівши дані до стеку, глибина якого визначена відповідно до варіанту №9.
Стек (stack) - лінійний список, у якому всі видалення й доповнення (і звичайно всякий доступ) робляться з одного кінця списку. Стек - частина пам'яті ОЗУ комп'ютера, що призначається для тимчасового зберігання байтів, використовуваних мікропроцесором; при цьому використається порядок запам'ятовування байтів “останнім увійшов - першим вийшов”, оскільки таке добавлення й видалення організовувати простіше всього, то операції здійснюються дуже швидко. Дії зі стеком виконуються за допомогою регістра покажчика стека. Будь-яке ушкодження цієї частини пам'яті приводить до фатального збою. Стек у вигляді списку (pushdown list) - стек, організований таким чином, що останній елемент, що вводить в область пам'яті, розміщується на вершині списку. З стека ми завжди виключаємо "молодший" елемент із наявних у списку, тобто той, котрий був включений пізніше інших. Для черги справедливо в точності протилежне правило: видаляється завжди "старший" елемент; вузли залишають список у тім порядку, у якому вони в нього ввійшли. Стеки дуже часто зустрічаються в практиці. Простим прикладом може послуговувати ситуація, коли ми переглядаємо безліч даних і утворюємо список особливих станів або об'єктів, які повинні оброблятися пізніше; коли первісна безліч оброблена, ми повертаємося до даного списку й виконуємо наступну обробку, видаляючи елементи зі списку, поки список не стане порожнім. Для цієї мети придатні як стек, так і черга, але стек, як правило, зручніший. При вирішенні завдань наш мозок поводиться як "стек": одна проблема приводить до іншої, а та у свою чергу до наступної; ми накопичуємо в стеці ці завдання й підзавдання й забуваємо про них у міру того, як вони вирішуються. Аналогічно процес входів у підпрограми й виходів з них при виконанні машинної програми подібний до процесу функціонування стека. Стеки особливо корисні при обробці мов, що мають структуру вкладень. Взагалі, стеки найчастіше виникають у зв'язку з алгоритмами, що мають явно або неявно рекурсивний характер.
У стеці елемент додаються й віддаляються тільки з одного кінця. На малюнку це елемент N. Тобто якщо він додався, то видалятися може спочатку тільки він, а вже потім всі інші. Для стеку характерні такі властивості:
елементи додаються у вершину (голову) стеку;
елементи видаляються з вершини (голови) стеку;
покажчик в останньому елементі стеку дорівнює NULL;
неможливо вилучити елементи стеку, не вилучивши всі елементи, що йдуть попереду. Стек можна уявити собі як коробці, у яку складають які-небудь предмети, щоб дістати самий нижній потрібно попередньо витягти інші. Стек можна вподібнити стопці тарілок, з якої можна взяти верхню й на яку можна покласти нову тарілку. [Інша назва стека в літературі - “магазин” - зрозуміло всякому, хто розбирав автомат Калашникова]. У програмуванні стеки мають широке застосування. Наприклад під час виклику підпрограми адрес повернення до неї зберігається у стеку. У випадку, коли відбувається цілий ряд послідовних викликів, адреси повернення розміщаються в стеці в порядку останнім прийшов - першим вийшов, так що після завершення виконання кожної функції відбувається перехід до функції, її що викликала. Стек підтримує як звичайні нерекурсивні виклики, так і рекурсивний виклик функцій. Стек використовується компілятором під час обчислення виразів, до нього записуються значення локальних змінних тощо.
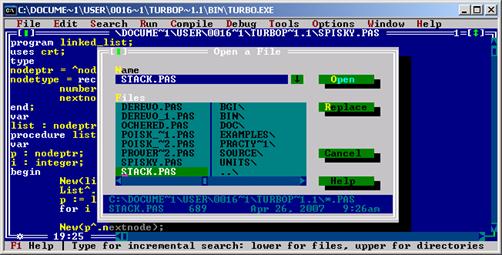
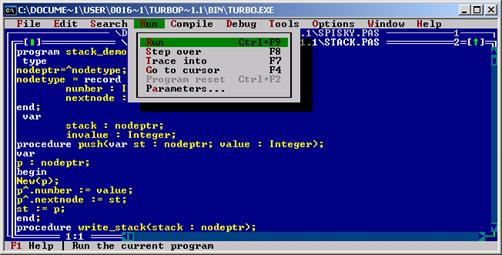
4. Вводимо дані черги
Виконати її, ввівши дані до черги, довжина якої визначена відповідно до варіанту №9. Черга (queue) - лінійний список, у якому всі видалення відбуваються на одному кінці списку, а всі включення (і звичайно всякий доступ) робляться на іншому його кінці. Черга - тип даних, при якому нові дані розташовуються слідом за існуючими в порядку надходження; першими дані, що надійшли, при цьому обробляються першими. У деяких розділах математики слово "чергу" використовують у більше широкому змісті, позначаючи будь-який сорт списку, у якому наявні видалення й додавання; зазначені вище спеціальні випадки називаються тоді "чергами з різними дисциплінами". Однак тут термін "черга" використовується у більш вузькому змісті, аналогічному впорядкованим чергам людей, що очікують обслуговування. Правило тут таке ж, як у живій черзі: першим прийшов - першим тебе і обслужений. Прийшов новий покупець, встав (добавився) у кінець черги, а який уже зробив покупки пішов (вийшов) з початку черги. Тобто першим прийшов, першим пішов. Інакше кажучи, у черги є голова (head) і хвіст (tail). Елемент, що додається в чергу, виявляється в її хвості. У черзі новий елемент додається тільки з одного кінця. Видалення елемента відбувається на іншому кінці. Черга, це по суті однонаправлений список, тільки додавання й видалення елементів відбувається на кінцях списку. Черга характеризується такими властивостями: · елементи додаються в кінець черги; · елементи зчитуються та видаляються з початку (вершини) черги; · покажчик в останньому елементі черги дорівнює NULL; · неможливо отримати елемент із середини черги, не вилучивши все елементи що ідуть попереду. Наведемо приклади застосування черг в обчислювальній техніці. У мережній операційній системі процесор сервера обслуговує в певний момент часу тільки одного користувача. Запити інших користувачів записуються до черги. Під час обслуговування користувачів кожен запит просувається до початку черги. Перший в черзі запит підлягає "першочерговому" обслуговуванню. У комп'ютерній мережі за чергою обслуговуються інформаційні пакети. Черги застосовуються також для буферизації потоків даних, що виводяться на друк, якщо в комп'ютерній мережі використовується один принтер. Крім цих структур існують і інші, наприклад деки, двонаправленні списки, кільцеві списки і т. і. Ь На малюнку нище графічно зображено дек (deck) (стек із двома кінцями) - лінійний список, у якому всі додавання й видалення (і звичайно всякий доступ) робляться на обох кінцях списку. Дек по суті двонаправлений список. У зв'язаному списку (linked list) елементи лінійно впорядковані, але порядок визначається не номерами, як у масиві, а покажчиками, що входять до складу елементів списку. Списки є зручним способом зберігання динамічних даних, що дозволяють реалізувати всі операції, (хоча й не завжди ефективно). Інакше кажучи, елемент двостороннє зв'язаного списку (doubly linked list) - це запис, що містить три поля: key (ключ) і два покажчики - next (наступний) і prev (від previous-попередній). Крім цього, елементи списку можуть містити додаткові дані. Якщо х - елемент списку, то next вказує на наступний елемент списку, а prev - на попередній. Якщо prev{х}=nil, то в елемента х немає попереднього: це голова (head) списку. Якщо next{х}= nil, то х - останній елемент списку або, як говорять, його хвіст (tail). Ці дані є неявно загальноприйнятими в програмуванні. Звичайно, динамічні структури даних не обмежуються наведеними вище. Існують і інші, зокрема графи, дерева що займають свою окрему нішу у програмуванні і почасти вирішення певних питань не можливе без їх застосування.
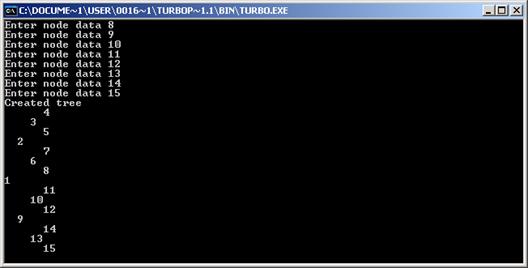
Виконати її, створивши бінарне дерево, кількість вузлів якого визначена відповідно до варіанту №15. Навести зображення дерева. Деревоподібна архітектура має найменший діаметр серед всіх існуючих, який дорівнює для бінарного дерева 2lg ( (P+1) /2) - відстань між двома листами, шлях між якими проходить через корінь. Для k-арних дерев діаметр зменшується зі збільшенням k. Недоліком деревоподібних мереж є те, що обмін даними між процесами відбувається за лінійний час, а процес-корінь є вузьким горлом при передачі інформації. Багатопроцесорний комп'ютер з паралельною обробкою інформації називається деревовидною машиною (tree machine) [33], якщо його процесори сполучені зв'язками так, що утворюється топологія повного бінарного дерева. Такий комп'ютер має 2d-1 процесорних елементів для деякого d, які розбиті на d рівнів, пронумерованих від 1 до d. Кожний процесор на рівні j, 1ЈjЈd, зв'язаний з єдиним процесором на рівні j-1 (батьком), та з двома процесорами на рівні j+1 (синами). Зв'язки між процесами розташовані таким чином, що безпосередньо обмінюватися інформацією можуть лише батько з сином. Єдиний процесор на першому рівні називається коренем в топології дерева, а процесори на рівні d - листами. Корінь не має батька, а листи не мають синів. На малюнку 15 зображена топологія деревовидної машини з d=4 рівнями, яка містить 24-1 = 15 процесорних елементів.
Висновок
У виконаній роботі було розглянуто процеси пошуку інформацій та розроблено структури даних для ефективного зберігання та обробки інформації. Як приклад розглянуто бінарне дерево. Це динамічна структура даних, розмір якої обмежується тільки розміром віртуальної пам'яті комп'ютера. Бінарні дерева забезпечують пошук конкретного значення, максимуму, мінімуму, попереднього, наступного, операції вставки та видалення елемента. Розглянуті у роботі бінарні структури широко використовуються у житті, наприклад це різноманітні "ієрархічні структури", які нині широко використовуються в багатьох комп'ютерних завданнях. На даний час також розвивається граматичний аналіз, в основі якого і знаходяться принципи бінарних дерев. Граматичний аналіз на даний час широко використовується у сучасних пошукових алгоритмах.
Список використаної літератури
1. Баррон Д. Рекурсивные методы в программировании, - М.: 1974
2. Дмитриева М.В., Кубенский А.А. Элементы современного программирования, - СПб.: 1991.
3. Барашенков В.В. Анализ и преобразование операторных схем алгоритмов: учебное пособие. - Л.: ЛЭТИ, 1979.
4. Кинг Д. Создание еффективного программного обеспечения. - М.: Мир, 1991.
5. Барашенков В.В. Интерпретация операторных схем алгоритмов. - Л.: ЛЭТИ, 1978.
6. Бентли Дж. Жемчужины творчества программистов. - М.: Мир, 1990.
7. Шауман А.М. Основы машинной арифметики. - 1979.
8. Ахо, Альфред В. и др. Построение и анализ вычислительных алгоритмов. - М.: Мир, 1979
9. Криницкий Н.А. Программирование и алгоритмические языки. - 1975.
10. Прикладные вопросы системного анализа. Межвузовский тематический сборник. Вып.2. Куйбышев, 1976.
11. Автоматическое построение ассоциативного списка со сжатием информации. - К., 1976.
12. Квиттнер П. Задачи, программы, вычисления, результаты. - М.: Мир, 1980.
13. Шауман А.М. Основы машинной арифметики. - 1979.
14. Малоземов В.Н. Певный А.Б. Рекуррентные вычисления. - Л., изд. ун-та, 1976.


