Быстрый поиск

Дипломная работа: Моделирование конкурентоспособности товара на современном рынке

Ограничения:

, ;

, , .

Дополнительное условие:

Функция показывает каково будет распределение средств (у. е.) по различным параметрам , , :

– для улучшения технических характеристик ;

– для понижения экономических параметров ;

– для достижения требуемых норм .

-число технических характеристик,

- число экономических характеристик,

- число нормативных параметров,

– общее число фирм на рынке.

3.2 Классификация задачи

Классифицируем поставленную математическую модель.

Практические задачи оптимизации, которые сводятся к математическим моделям вида: , , где множество допустимых значений определяется ограничениями-равенствами или ограничениями-неравенствами или , при -заданному множеству индексов, то они называются задачами математического программирования.

Если функции и - нелинейные и все управляемые переменные неотрицательны, то это задача нелинейного программирования. В нашей задаче существует особенность целевой функции – она является дробно-линейной функцией, а значит, мы рассматриваем задачу дробно-линейного программирования.

Такая задача сводится к задаче линейного программирования. Существует несколько наиболее часто используемых методов для решения задач линейного программирования, к ним относится графический метод, симплекс-таблица и различные разновидности симплекс-метода.

Графический метод неприменим из-за количества управляемых переменных, их слишком много. Допустимым множеством будет являться многогранник в мерном пространстве. Основная черта – наглядность – теряется.

Затруднения использования симплекс-метода связанны не только с той же проблемой, что у графического метода, к ней еще прибавляется сложность приведения к каноническому виду, представления в симплекс-таблицах.

Изменение управляемых переменных задано дискретным рядом значений, а значит, можем классифицировать поставленную задачу, как дискретную задачу оптимизации.

Часто применимый для таких задач метод ветвей и границ.

3.3 Метод оптимизации для решения поставленной задачи

Наиболее часто встречающийся, распространенный метод для решения такого типа задач – метод ветвей и границ.

3.3.1 Общее описание метода ветвей и границ

Метод применяется для решения разнообразных задач дискретной оптимизации. Его идея состоит в последовательном разбиении допустимого множества исходной задачи

, , – дискретно

на взаимно непересекающихся подмножествах (этот процесс называется ветвлением) и получении оценок снизу (границ) значений целевой функции на этих подмножествах (). При выполнении определенных условий процесс ветвления завершается и решение задачи на одном из подмножеств оказывается решением исходной задачи . Сказанное выше и объясняет название метода.

Схему поиска решения методом ветвей и границ в каждом конкретном случае можно наглядно представить в виде некоторого дерева, состоящего из множества вершин и соединяющих их ветвей.

Примеры деревьев:

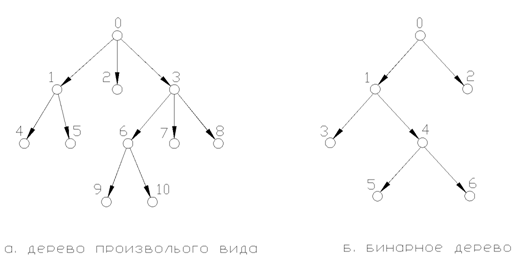
Начальной вершине 0 соответствует исходное допустимое множество или исходная задача (1), а любой другой вершине – подмножество , полученное в результате ветвления, или подзадача :

, .

Если при ветвлении из каждой вершины происходит разбиение соответствующего ей множества на две части, то схема метода изображается бинарным деревом.

Процесс ветвления из данной вершины не производится, если выполнено одно из условий:

. Граница найдена точно: , т.е. получено решение подзадачи . Будем говорить, что в этом случае вместо оценки решения в вершине найдено полное решение , соответствующее этой вершине.

. Множество является пустым.

. Из полученных до этого полных решений найдется такое , что граница удовлетворяет неравенству

В данном случае дальнейший поиск решения исходной задачи на подмножестве не имеет смысла, и говорят, что вершина «убита» вершиной . В самом деле, из следует, что , т.е. минимальное значение функции на не может быть меньше, чем в уже найденной точке .

Вершины, удовлетворяющие одному из условий – , назовем прозондированными. Непрозондированные вершины, из которых ветвление еще не произведено, будем называть активными, а совокупность всех таких вершин – активным множеством .

Процесс ветвления продолжается до тех пор, пока остается хотя бы одна активная вершина, т.е. . По окончании процедуры ветвления можно указать решение исходной задачи – это то из найденных полных решений , для которого значение минимально.