Реферат: Метод экспертных оценок

                                                                                                                    (5.18)

Рассмотрим вначале суммированные по i при фиксиро­ванном  j. Это есть сумма рангов для j-го эксперта. По­скольку эксперт использует для ранжировки натураль­ные числа от 1 до n, то, как известно, сумма натураль­ных чисел от 1 до n  равна [12]

                                                                                                                 (5.19)

Подставляя (5.19) в (5.18), получаем [12]

                                                                                                  (5.20)

Таким образом, среднее значение зависит только от числа экспертов m и числа объектов n.

Для вычисления максимального значения оценки дис­персии подставим в (5.15) значение  из (5.14) и воз­ведем в квадрат двучлен в круглой скобке. В результате получаем [12]

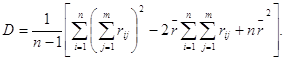                                                                       (5.21)

Учитывая, что из (5.18) следует

получаем [12]

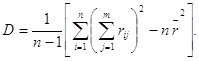                                                                                           (5.22)

Максимальное значение дисперсии достигается при наибольшем значении первого члена в квадратных скоб­ках. Величина этого члена существенно зависит от рас­положения рангов - натуральных чисел в каждой стро­ке i. Пусть, например, все m экспертов дали одинаковую ранжировку для всех n объектов. Тогда в каждой строке матрицы будут расположены одинаковые числа. Следовательно, суммирование рангов в каждой i-u стро­ке дает m-кратное повторение i-ro числа [12]:

Возводя в квадрат и суммируя по i, получаем значение первого члена в (5.22) [12]:

                                                                             (5.23)

Теперь предположим, что эксперты дают несовпадающие ранжировки, например, для случая n=m все эксперты присваивают разные ранги одному объекту. Тогда [12]

     

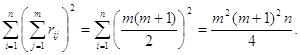
Сравнивая это выражение с  при m=n, убеждаемся, что первый член в квадратных скобках формулы (9) ра­вен второму члену и, следовательно, оценка дисперсии равна нулю.

Таким образом, случай полного совпадения ранжиро­вок экспертов соответствует максимальному значению оценки дисперсии. Подставляя (5.23) в (5.22) и выпол­няя преобразования, получаем [12]

                                                                                                            (5.24)

Введем обозначение [12]

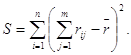                                                                                                            (5.25)

Используя (5.25), запишем оценку дисперсии (5.15) в виде [12]

                                                                                                                        (5.26)

Подставляя (5.24), (5.25), (5.26) в (5.17) и сокращая на множитель (n—1), запишем окончательное выражение для коэффициента конкордации [12]

                                                                                                                (5.27)

Данная формула определяет коэффициент конкордации для случая отсутствия связанных рангов.

Если в ранжировках имеются связанные ранги, то максимальное значение дисперсии в знаменателе форму­лы (5.17) становится меньше, чем при отсутствии свя­занных рангов. Можно показать, что при наличии свя­занных рангов коэффициент конкордации вычисляется по формуле [12]:

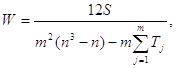                                                                                                 (5.28)

где

                                                                                                                 (5.29)

В формуле (5.28)  - показатель связанных рангов в j-й ранжировке,  - число групп равных рангов в j-й ран­жировке,  - число равных рангов в k-й группе связан­ных рангов при ранжировке j-м экспертом. Если совпа­дающих рангов нет, то =0, =0 и, следовательно, =0. В этом случае формула (5.28) совпадает с форму­лой (5.27).

Коэффициент конкордации равен 1, если все ранжи­ровки экспертов одинаковы. Коэффициент конкордации равен нулю, если все ранжировки различны, т. е. со­вершенно нет совпадения.

Коэффициент конкордации, вычисляемый по формуле (5.27) или (5.28), является оценкой истинного значения коэффициента и, следовательно, представляет собой случайную величину. Для определения значимости оценки коэффициента конкордации необходимо знать распреде­ление частот для различных значений числа экспертов m и количества объектов n. Распределение частот для W при  и вычислено в [52]. Для боль­ших значений m и n можно использовать известные ста­тистики. При числе объектов n>7 оценка значимости коэффициента конкордации может быть произведена по критерию . Величина Wm(n—1) имеет  распределе­ние с v=n –1 степенями свободы.

При наличии связанных рангов  распределение с v=n—1 степенями свободы имеет величина [12]:

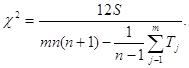                                                                                              (5.30)

Энтропийный коэффициент конкордации определяет­ся формулой (коэффициент согласия) [12]:

                                                                                                                    (5.31)

где Н – энтропия, вычисляемая по формуле

                                                                                                        (5.32)

а - максимальное значение энтропии. В формуле для энтропии  - оценки вероятностей j-го ранга, при­сваиваемого i-му объекту. Эти оценки вероятностей вы­числяются в виде отношения количества экспертов , приписавших объекту  ранг j к общему числу экспер­тов [12].

                                                                                                                           (5.33)

Максимальное значение энтропии достигается при равновероятном распределении рангов, т. е. когда . Тогда [12]

                                                                                                                     (5.34)

Подставляя это соотношение в формулу (5.32), получаем [12]

                                                                                              (5.35)

Коэффициент согласия изменяется от нуля до едини­цы. При  расположение объектов по рангам рав­новероятно, поскольку в этом случае . Данный случай может быть обусловлен либо невозможностью ранжировки объектов по сформулированной совокупно­сти показателей, либо полной несогласованностью мне­ний экспертов. При , что достигается при нулевой энтропии (H=0), все эксперты дают одинаковую ранжи­ровку. Действительно, в этом случае для каждого фик­сированного объекта  все эксперты присваивают ему один и тот же ранг j, следовательно, , a   Поэтому и H=0.

Страницы: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10